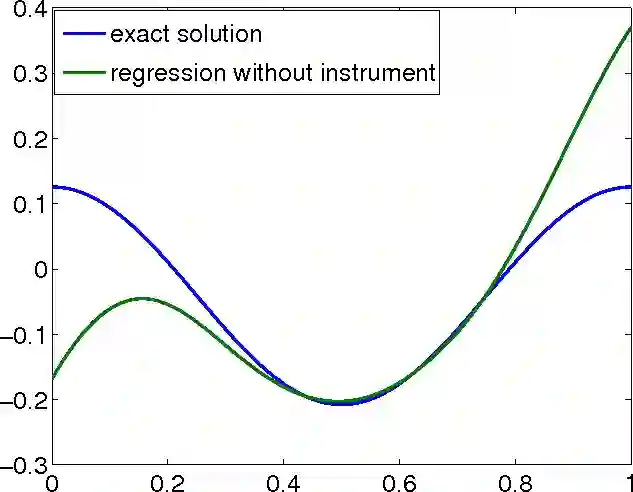
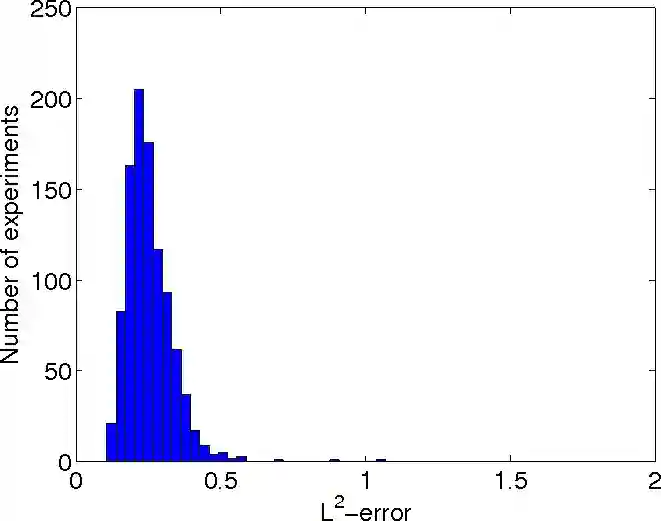
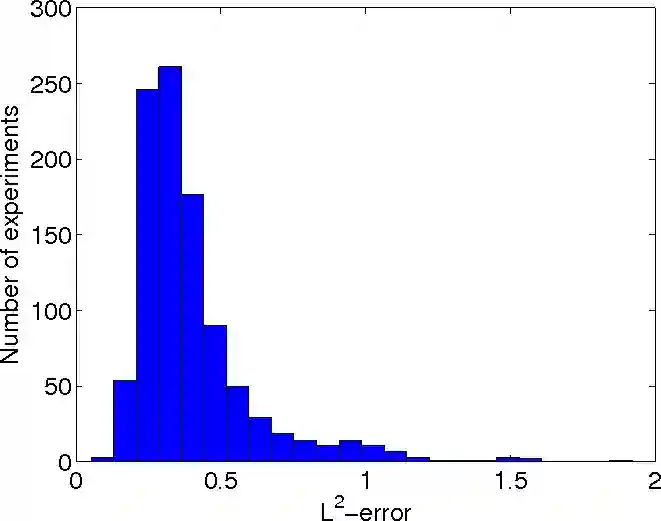
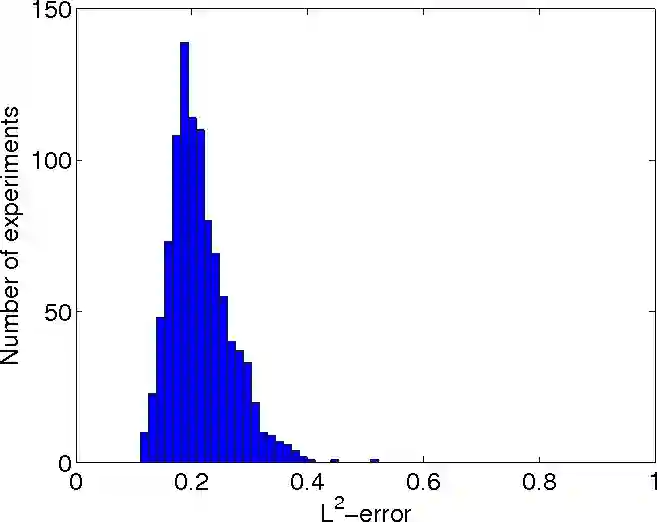
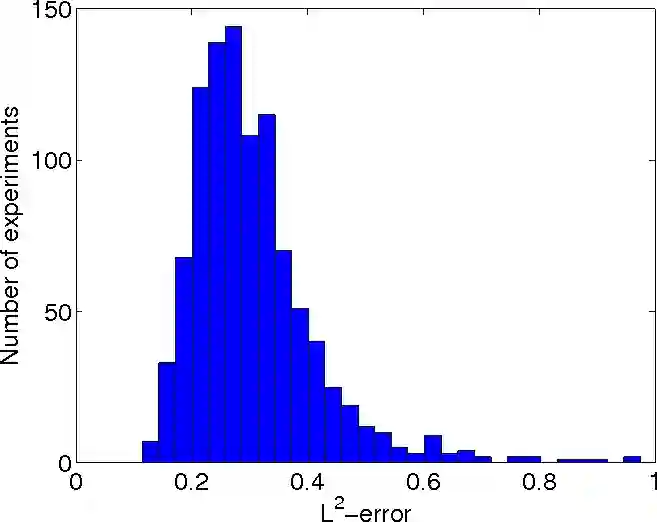
The problem of endogeneity in statistics and econometrics is often handled by introducing instrumental variables (IV) which fulfill the mean independence assumption, i.e. the unobservable is mean independent of the instruments. When full independence of IV's and the unobservable is assumed, nonparametric IV regression models and nonparametric demand models lead to nonlinear integral equations with unknown integral kernels. We prove convergence rates for the mean integrated square error of the iteratively regularized Newton method applied to these problems. Compared to related results we derive stronger convergence results that rely on weaker nonlinearity restrictions. We demonstrate in numerical simulations for a nonparametric IV regression that the method produces better results than the standard model.
翻译:统计和计量经济学的内分质问题往往通过引入满足平均独立假设的工具变量(四)来解决,即,不可观察的变量是平均独立于工具之外的。当假设四的完全独立和不可观察的模型完全独立时,非参数四的回归模型和非参数需求模型会导致具有未知整体内核的非线性整体方程式。我们证明适用于这些问题的迭代正规化的牛顿方法的平均合并方差的趋同率。与相关结果相比,我们得出了更强大的趋同结果,依赖于较弱的非线性限制。我们在数字模拟中证明,该方法产生比标准模型更好的结果。