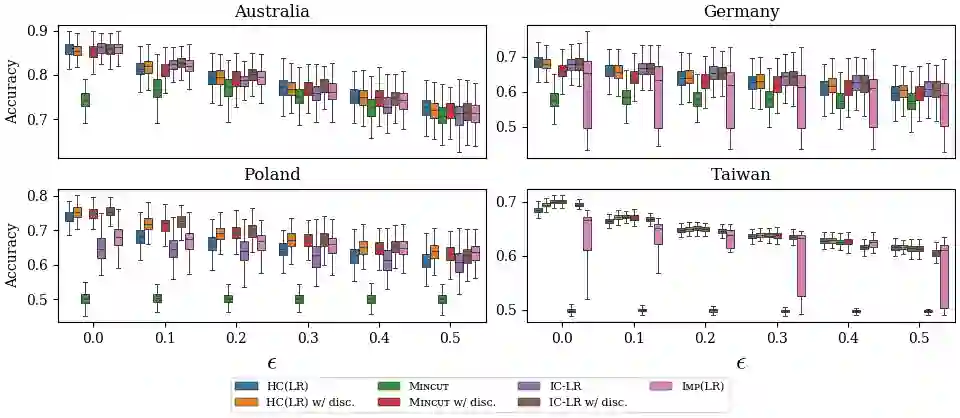
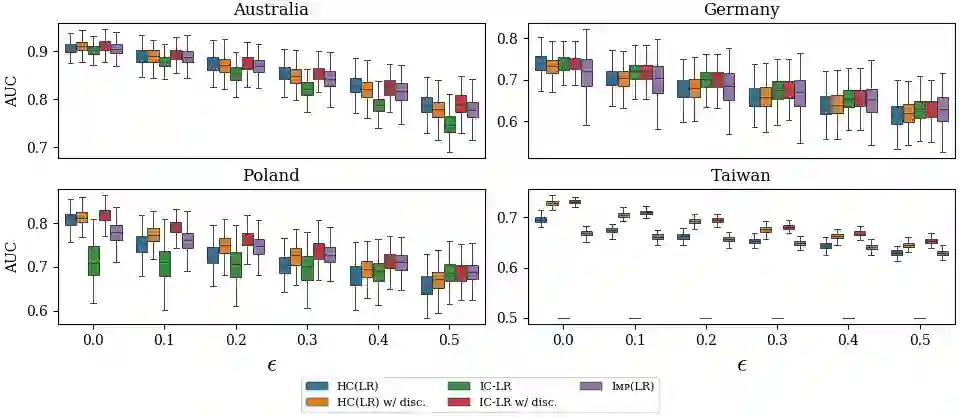
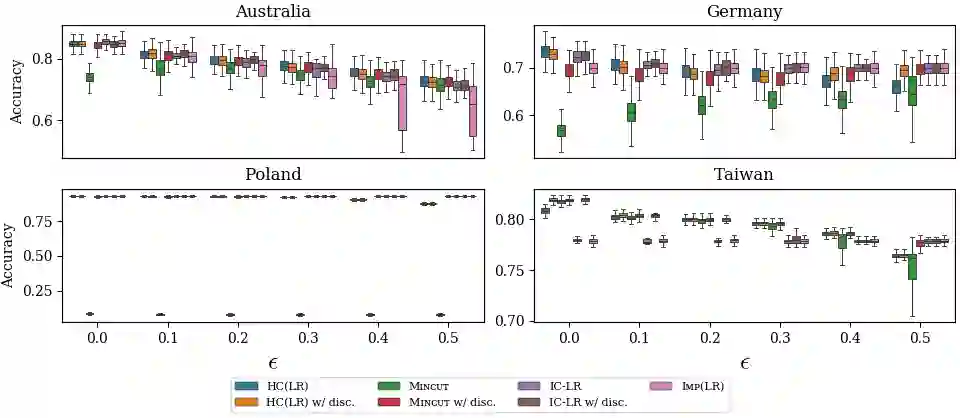
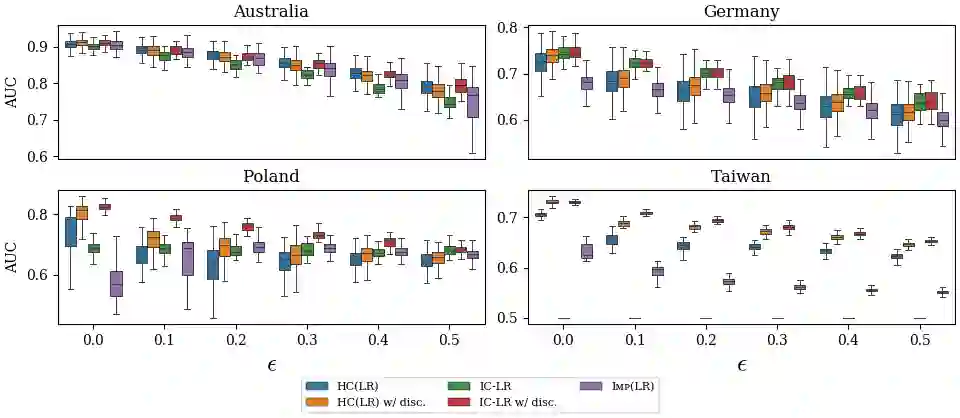
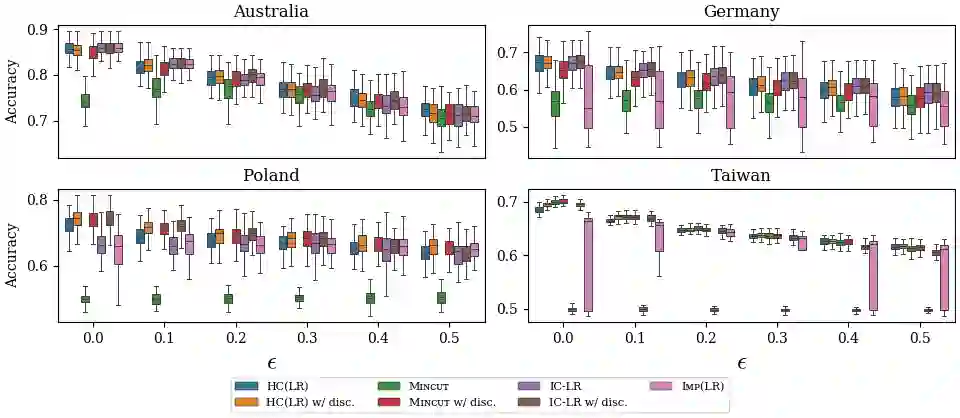
Machine learning techniques can be useful in applications such as credit approval and college admission. However, to be classified more favorably in such contexts, an agent may decide to strategically withhold some of her features, such as bad test scores. This is a missing data problem with a twist: which data is missing {\em depends on the chosen classifier}, because the specific classifier is what may create the incentive to withhold certain feature values. We address the problem of training classifiers that are robust to this behavior. We design three classification methods: {\sc Mincut}, {\sc Hill-Climbing} ({\sc HC}) and Incentive-Compatible Logistic Regression ({\sc IC-LR}). We show that {\sc Mincut} is optimal when the true distribution of data is fully known. However, it can produce complex decision boundaries, and hence be prone to overfitting in some cases. Based on a characterization of truthful classifiers (i.e., those that give no incentive to strategically hide features), we devise a simpler alternative called {\sc HC} which consists of a hierarchical ensemble of out-of-the-box classifiers, trained using a specialized hill-climbing procedure which we show to be convergent. For several reasons, {\sc Mincut} and {\sc HC} are not effective in utilizing a large number of complementarily informative features. To this end, we present {\sc IC-LR}, a modification of Logistic Regression that removes the incentive to strategically drop features. We also show that our algorithms perform well in experiments on real-world data sets, and present insights into their relative performance in different settings.
翻译:机器学习技巧在信用审批和大学录取等应用中可能有用。 但是, 要在这种背景下更有利地分类, 代理商可能会决定从战略上保留她的一些特征, 比如测试分数差。 这是一个缺少的数据问题, 是一个扭曲的问题: 当数据真实分布完全为人所知时, 缺少哪些数据? 因为特定的分类器可能会产生抑制保留某些特性值的动力。 我们处理培训对这种行为具有强健性的分类师的问题。 我们设计了三种分类方法 : prsc Minc}, rsc Hill- Climbing} ( ~c HC} ) 和 激励性可兼容的物流回归( hC- LR} ) 。 我们发现, 当数据真实分布完全为已知时, hsc Mincultip} 是最佳的。 但是, 它可以产生复杂的决定界限, 在某些情况下很容易被过度适应。 基于真实的分类师的特征( 即没有战略隐藏特性的缩略图 ), 我们设计了一个更简单的替代品叫做 rc- c 相对 HC} 。