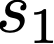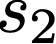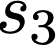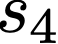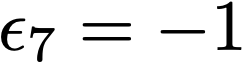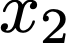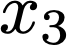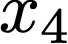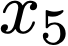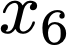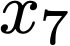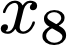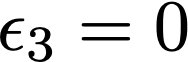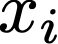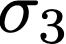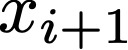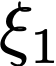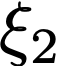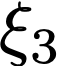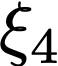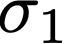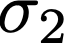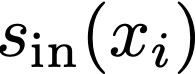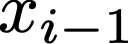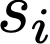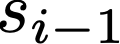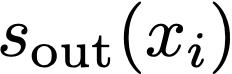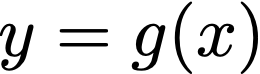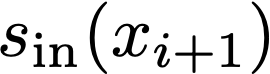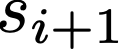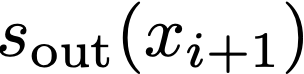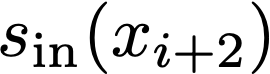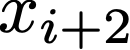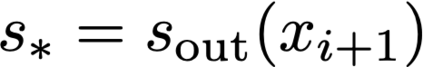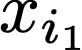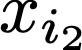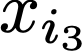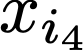Ridgeless Interpolation with Shallow ReLU Networks in $1D$ is Nearest Neighbor Curvature Extrapolation and Provably Generalizes on Lipschitz Functions

We prove a precise geometric description of all one layer ReLU networks $z(x;\theta)$ with a single linear unit and input/output dimensions equal to one that interpolate a given dataset $\mathcal D=\{(x_i,f(x_i))\}$ and, among all such interpolants, minimize the $\ell_2$-norm of the neuron weights. Such networks can intuitively be thought of as those that minimize the mean-squared error over $\mathcal D$ plus an infinitesimal weight decay penalty. We therefore refer to them as ridgeless ReLU interpolants. Our description proves that, to extrapolate values $z(x;\theta)$ for inputs $x\in (x_i,x_{i+1})$ lying between two consecutive datapoints, a ridgeless ReLU interpolant simply compares the signs of the discrete estimates for the curvature of $f$ at $x_i$ and $x_{i+1}$ derived from the dataset $\mathcal D$. If the curvature estimates at $x_i$ and $x_{i+1}$ have different signs, then $z(x;\theta)$ must be linear on $(x_i,x_{i+1})$. If in contrast the curvature estimates at $x_i$ and $x_{i+1}$ are both positive (resp. negative), then $z(x;\theta)$ is convex (resp. concave) on $(x_i,x_{i+1})$. Our results show that ridgeless ReLU interpolants achieve the best possible generalization for learning $1d$ Lipschitz functions, up to universal constants.