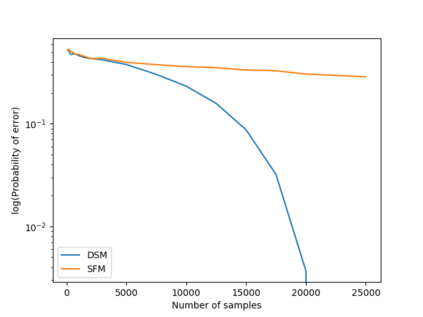
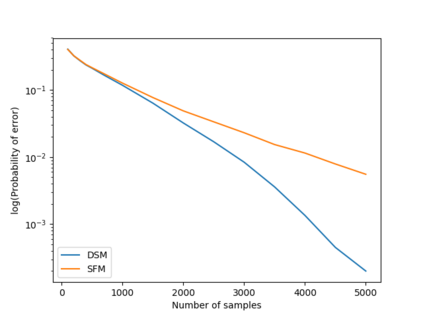
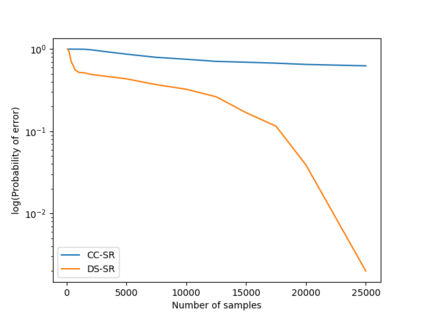
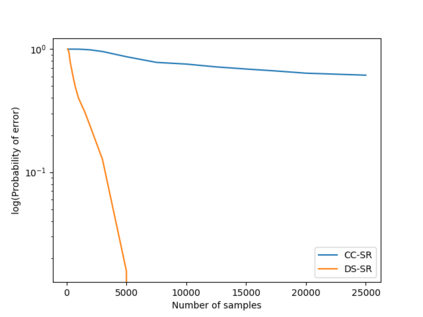
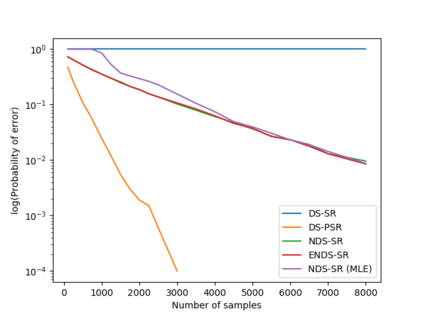
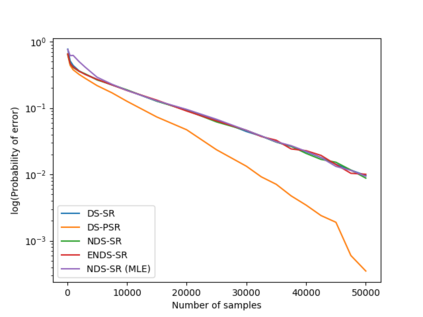
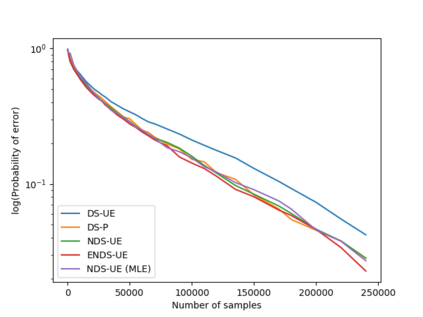
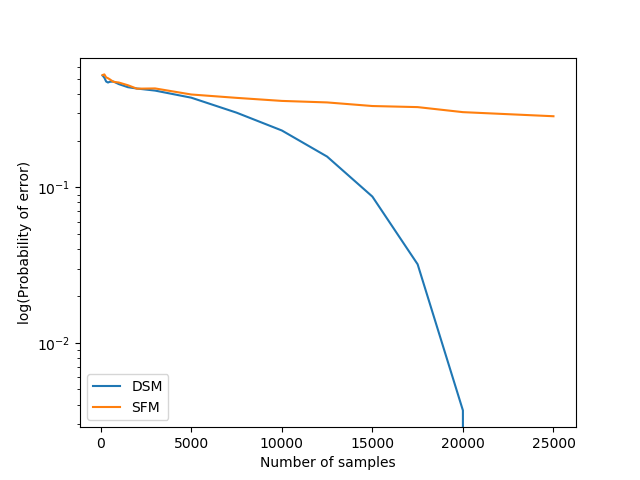
We consider a population, partitioned into a set of communities, and study the problem of identifying the largest community within the population via sequential, random sampling of individuals. There are multiple sampling domains, referred to as \emph{boxes}, which also partition the population. Each box may consist of individuals of different communities, and each community may in turn be spread across multiple boxes. The learning agent can, at any time, sample (with replacement) a random individual from any chosen box; when this is done, the agent learns the community the sampled individual belongs to, and also whether or not this individual has been sampled before. The goal of the agent is to minimize the probability of mis-identifying the largest community in a \emph{fixed budget} setting, by optimizing both the sampling strategy as well as the decision rule. We propose and analyse novel algorithms for this problem, and also establish information theoretic lower bounds on the probability of error under any algorithm. In several cases of interest, the exponential decay rates of the probability of error under our algorithms are shown to be optimal up to constant factors. The proposed algorithms are further validated via simulations on real-world datasets.
翻译:我们考虑的是人口,分成一组社区,研究通过个人随机抽样来识别人口中最大群体的问题。有多个取样区域,称为\emph{boxes},这个区域也可以分割人口。每个框可以由不同社区的个人组成,每个框可以分散在多个框中。学习机构可以在任何时候从任何选定的框中随机抽取个人样本(与替代一起),在这样做时,代理人可以了解被抽样个人所属的社区,以及这个人是否以前曾被抽样过。该代理的目的是通过优化取样战略和决策规则来尽量减少在\emph{fixed预算}设置的最大社区中误认的可能性。我们建议和分析这一问题的新算法,并确立关于任何算法中误差概率的理论下限的信息。在几个感兴趣的情况下,根据我们算法,错误概率的指数衰减率被证明为最优于不变因素。拟议的算法通过真实世界的模拟数据进一步验证。