Data Fusion in a Two-stage Spatio-Temporal Model using the INLA-SPDE Approach

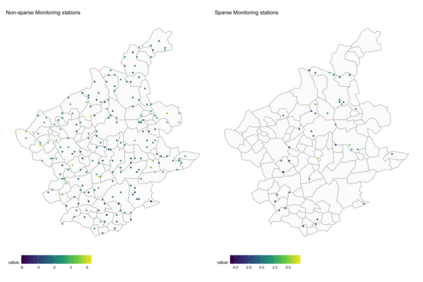
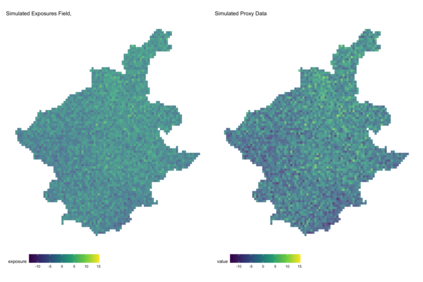
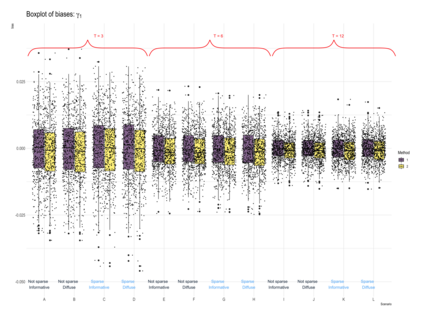
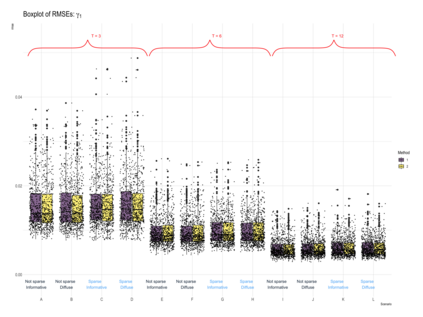
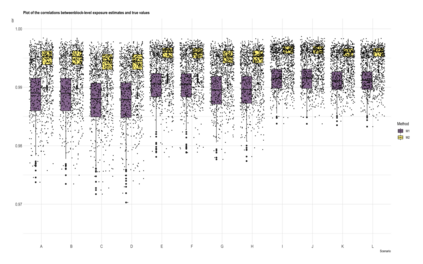
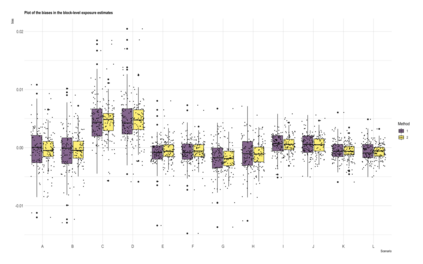
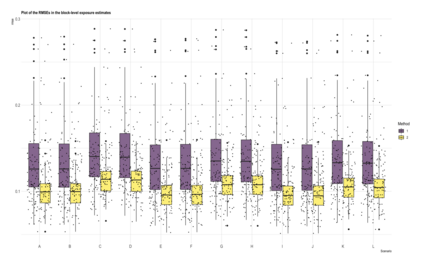
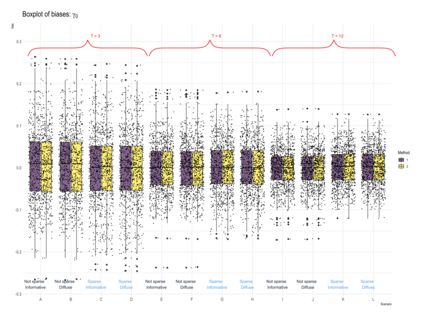
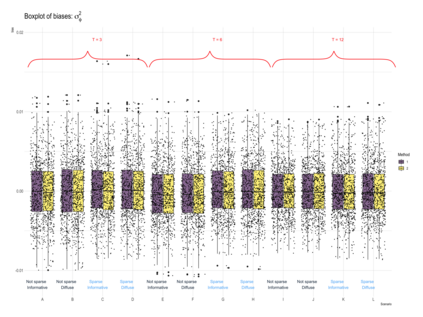
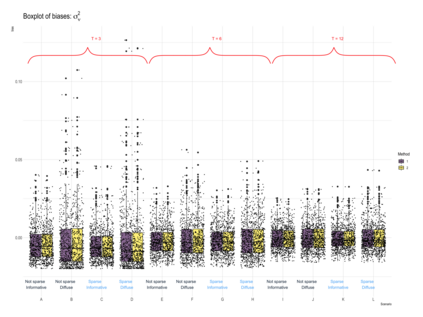
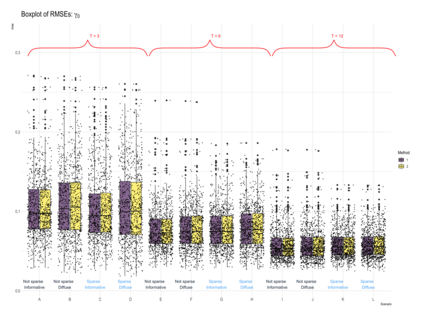
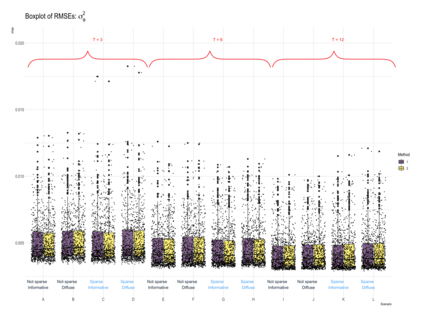
This paper proposes a two-stage estimation approach for a spatial misalignment scenario that is motivated by the epidemiological problem of linking pollutant exposures and health outcomes. We use the integrated nested Laplace approximation method to estimate the parameters of a two-stage spatio-temporal model; the first stage models the exposures while the second stage links the health outcomes to exposures. The first stage is based on the Bayesian melding model, which assumes a common latent field for the geostatistical monitors data and a high-resolution data such as satellite data. The second stage fits a GLMM using the spatial averages of the estimated latent field, and additional spatial and temporal random effects. Uncertainty from the first stage is accounted for by simulating repeatedly from the posterior predictive distribution of the latent field. A simulation study was carried out to assess the impact of the sparsity of the data on the monitors, number of time points, and the specification of the priors in terms of the biases, RMSEs, and coverage probabilities of the parameters and the block-level exposure estimates. The results show that the parameters are generally estimated correctly but there is difficulty in estimating the latent field parameters. The method works very well in estimating block-level exposures and the effect of exposures on the health outcomes, which is the primary parameter of interest for spatial epidemiologists and health policy makers, even with the use of non-informative priors.