A Unified Off-Policy Evaluation Approach for General Value Function

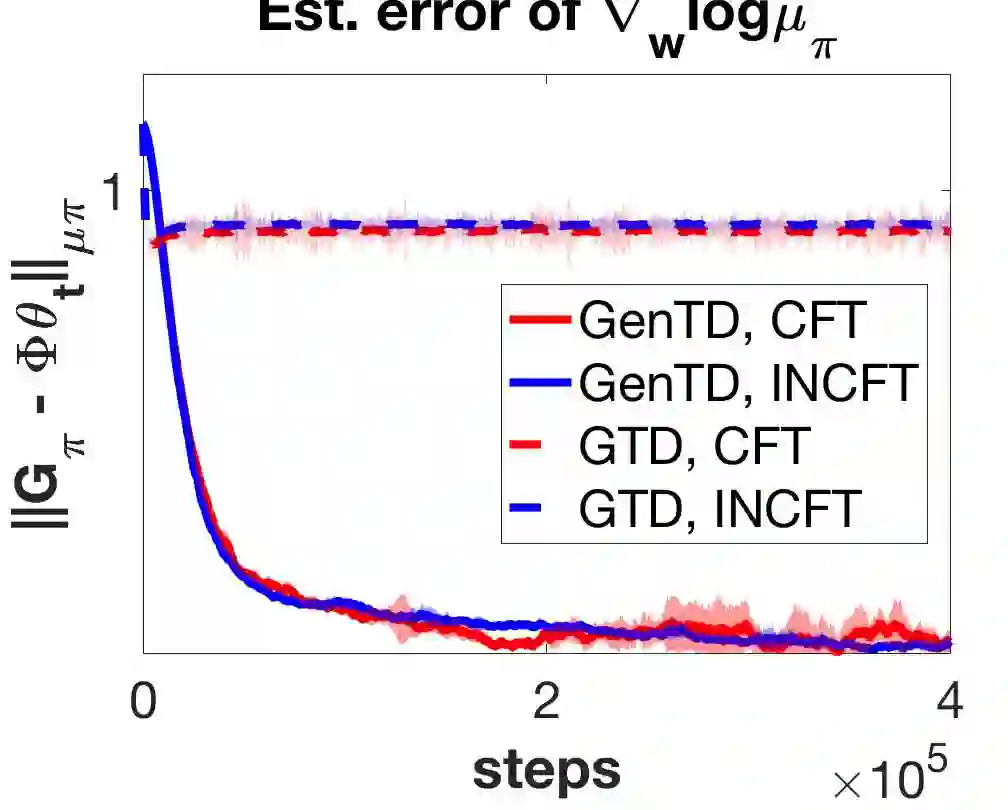
General Value Function (GVF) is a powerful tool to represent both the {\em predictive} and {\em retrospective} knowledge in reinforcement learning (RL). In practice, often multiple interrelated GVFs need to be evaluated jointly with pre-collected off-policy samples. In the literature, the gradient temporal difference (GTD) learning method has been adopted to evaluate GVFs in the off-policy setting, but such an approach may suffer from a large estimation error even if the function approximation class is sufficiently expressive. Moreover, none of the previous work have formally established the convergence guarantee to the ground truth GVFs under the function approximation settings. In this paper, we address both issues through the lens of a class of GVFs with causal filtering, which cover a wide range of RL applications such as reward variance, value gradient, cost in anomaly detection, stationary distribution gradient, etc. We propose a new algorithm called GenTD for off-policy GVFs evaluation and show that GenTD learns multiple interrelated multi-dimensional GVFs as efficiently as a single canonical scalar value function. We further show that unlike GTD, the learned GVFs by GenTD are guaranteed to converge to the ground truth GVFs as long as the function approximation power is sufficiently large. To our best knowledge, GenTD is the first off-policy GVF evaluation algorithm that has global optimality guarantee.