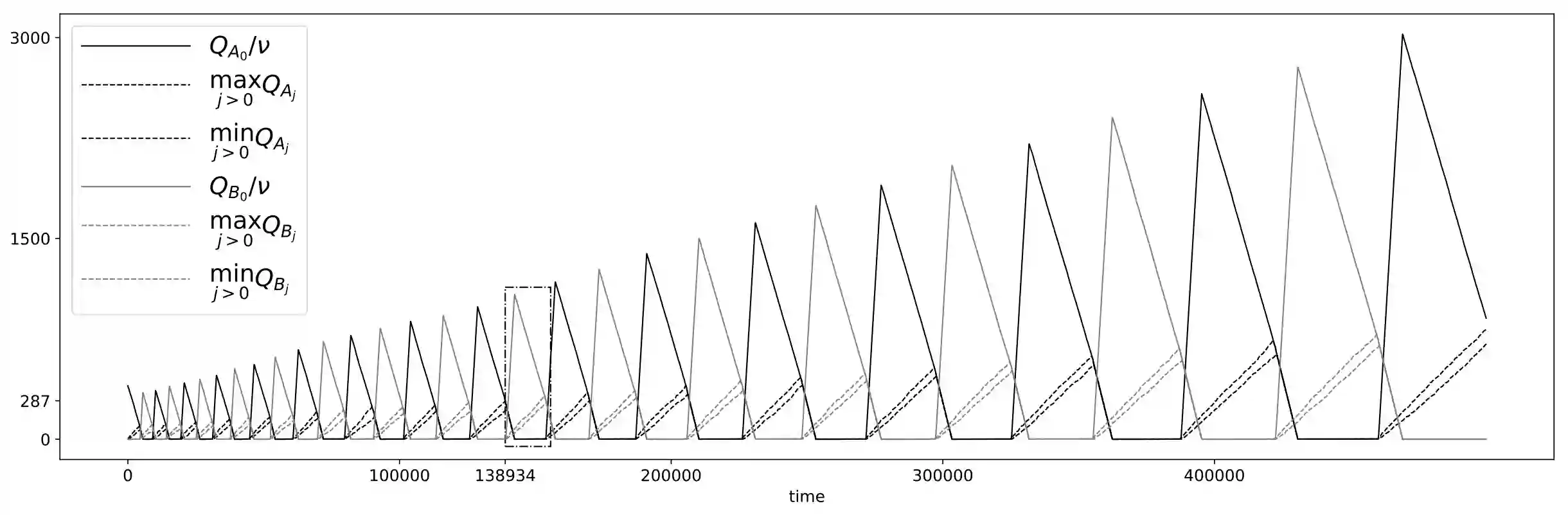
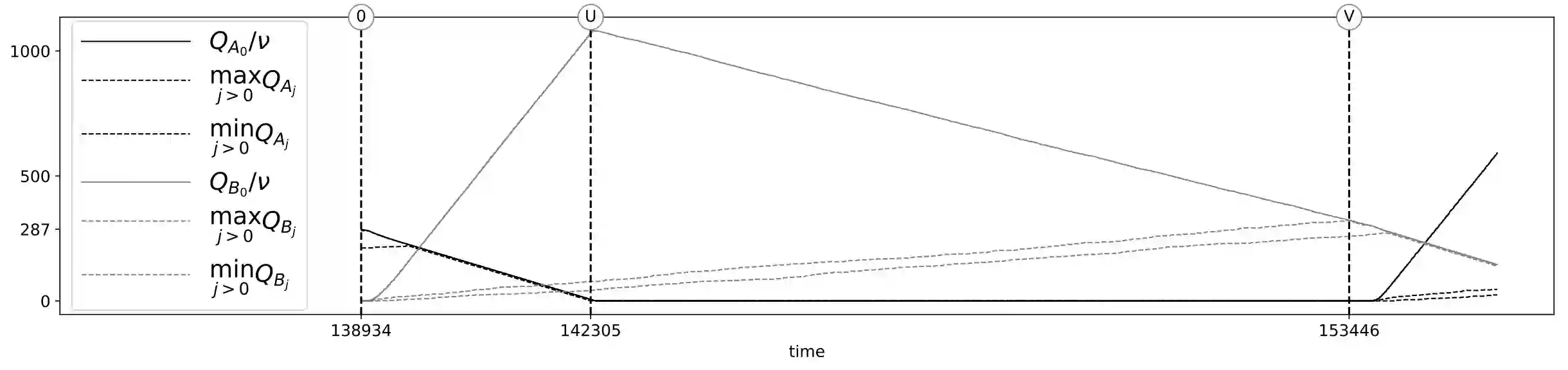
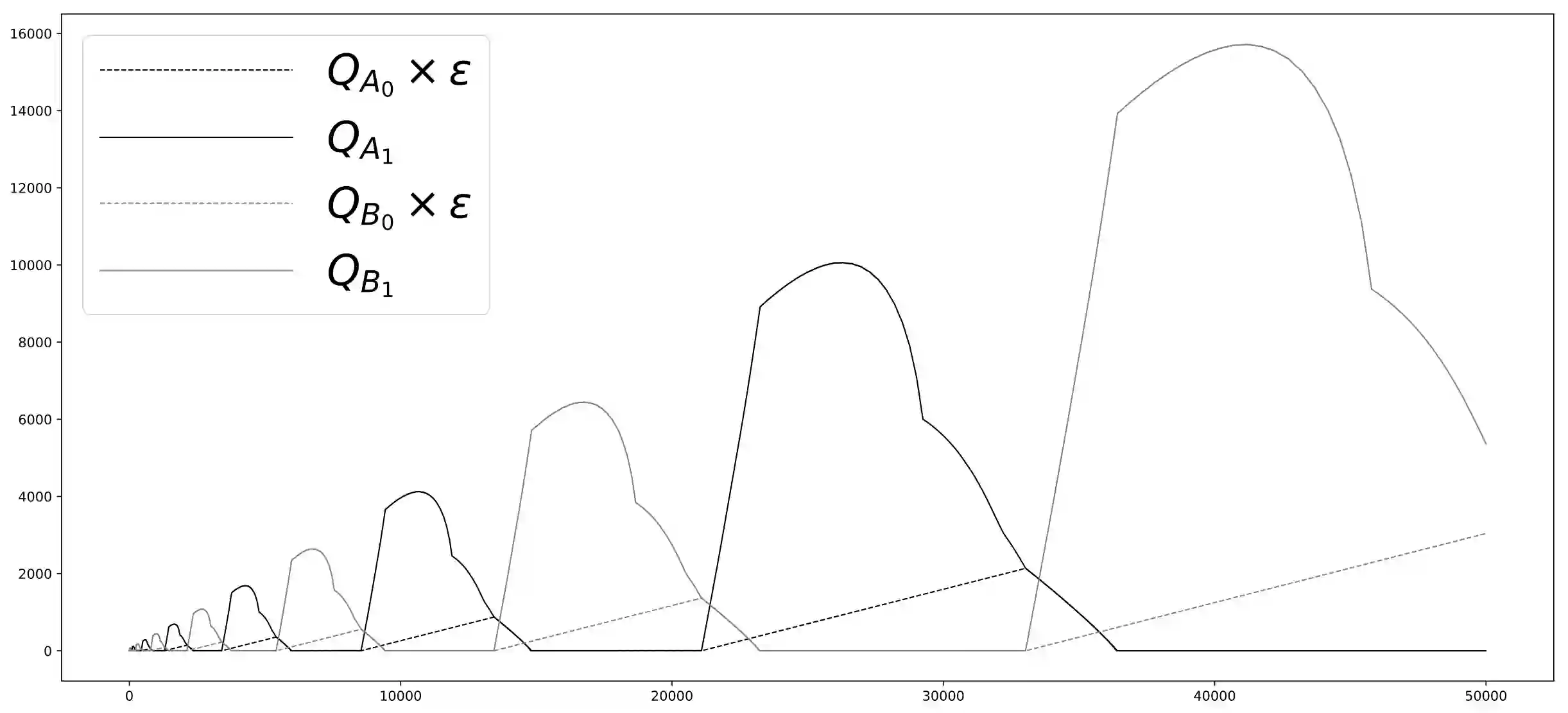
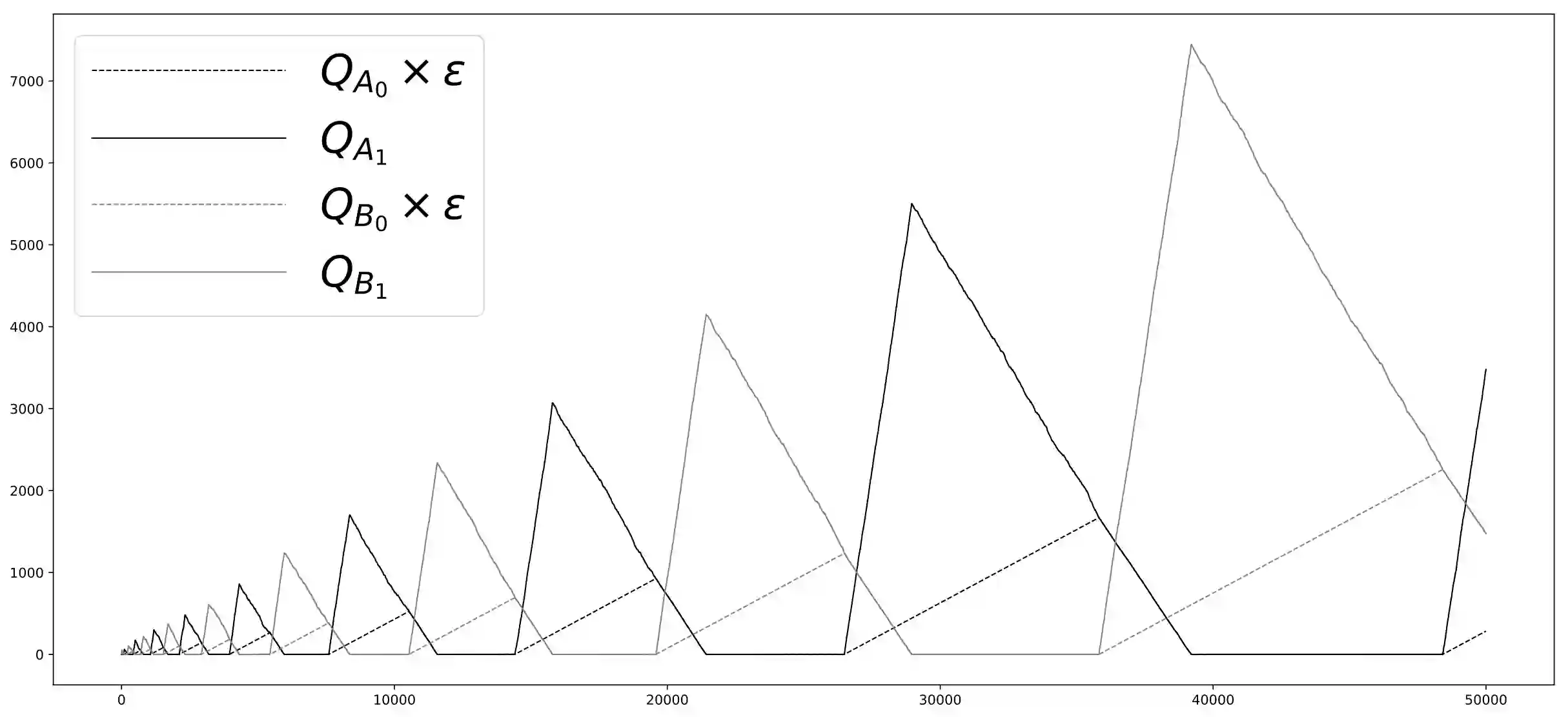
Consider a switched queueing network with general routing among its queues. The MaxWeight policy assigns available service by maximizing the objective function $\sum_j Q_j \sigma_j$ among the different feasible service options, where $Q_j$ denotes queue size and $\sigma_j$ denotes the amount of service to be executed at queue $j$. MaxWeight is a greedy policy that does not depend on knowledge of arrival rates and is straightforward to implement. These properties, as well as its simple formulation, suggest MaxWeight as a serious candidate for implementation in the setting of switched queueing networks; MaxWeight has been extensively studied in the context of communication networks. However, a fluid model variant of MaxWeight was shown by Andrews--Zhang (2003) not to be maximally stable. Here, we prove that MaxWeight itself is not in general maximally stable. We also prove MaxWeight is maximally stable in a much more restrictive setting, and that a weighted version of MaxWeight, where the weighting depends on the traffic intensity, is always stable.
翻译:考虑一个在队列之间有一般路由的换换队列网络。 MaxWeight 政策通过将目标函数$\sum_ j @ j\sigma_ j$最大化, 在不同可行的服务选项中分配了可用的服务, 目标函数$\sum_ j\ j\ sigma_ j$, $_j$ j$ 表示队列大小, 和$sgma_ j$ 表示要执行的服务量。 MaxWeight 是一个贪婪的政策, 不取决于对抵达率的了解, 并且可以直接执行。 这些属性及其简单表达方式, 表明 MaxWeight 是一个在设置被调换队列网络时执行的严肃候选对象; MaxWeight 已经在通信网络中进行了广泛的研究。 但是, Andrews- Zhang (2003) 显示的 MaxWeight 流体模型变体并不最稳定。 我们在这里证明 MaxWeight 本身不是一般最稳定。 我们还证明, 在更严格的环境中, MaxWeight 是最稳定的, 最稳定的, 而加权的版本, 而重的版本, 它的重量取决于取决于交通强度取决于交通强度。