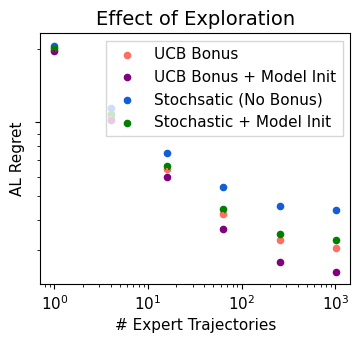
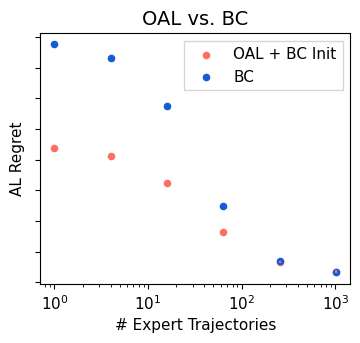
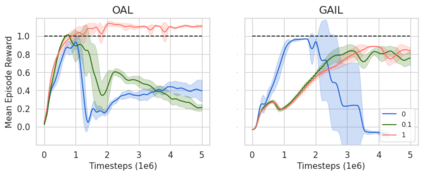
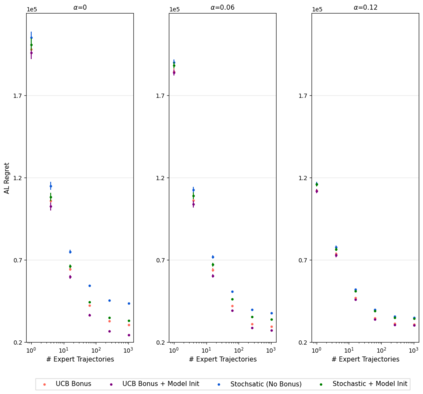
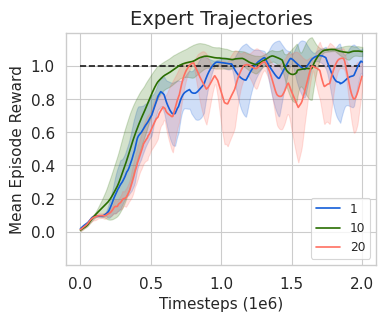
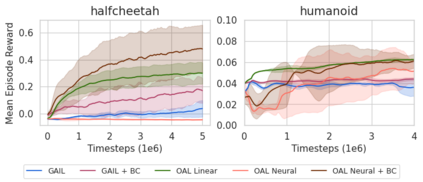
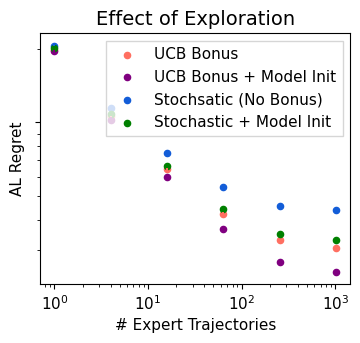
In Apprenticeship Learning (AL), we are given a Markov Decision Process (MDP) without access to the cost function. Instead, we observe trajectories sampled by an expert that acts according to some policy. The goal is to find a policy that matches the expert's performance on some predefined set of cost functions. We introduce an online variant of AL (Online Apprenticeship Learning; OAL), where the agent is expected to perform comparably to the expert while interacting with the environment. We show that the OAL problem can be effectively solved by combining two mirror descent based no-regret algorithms: one for policy optimization and another for learning the worst case cost. By employing optimistic exploration, we derive a convergent algorithm with $O(\sqrt{K})$ regret, where $K$ is the number of interactions with the MDP, and an additional linear error term that depends on the amount of expert trajectories available. Importantly, our algorithm avoids the need to solve an MDP at each iteration, making it more practical compared to prior AL methods. Finally, we implement a deep variant of our algorithm which shares some similarities to GAIL \cite{ho2016generative}, but where the discriminator is replaced with the costs learned by the OAL problem. Our simulations suggest that OAL performs well in high dimensional control problems.
翻译:在学徒学习(AL)中,我们得到了一个没有成本功能的Markov决定程序(MDP),我们没有获得成本功能。相反,我们观察的是由一位按照某些政策行事的专家抽样的轨迹。我们的目标是找到一种与专家在某些预定义的成本功能上的表现相匹配的政策。我们引入了AL(在线学徒学习;OAL)的在线变体(在线学徒学习;OAL),预计代理商在与环境互动时能够与专家的轨迹数量相对应。我们表明,OAL问题可以通过两种基于无回报的镜谱下行算法相结合来有效解决。一种基于政策优化的反向下行法,另一种用于学习最坏的个案成本。我们通过乐观的探索,我们得出一种与美元(sqrt{K}) 相匹配的算法,其中$(sqoqrt{K}) 是与MDP互动的次数,另外一种线性错误术语,取决于专家的轨迹数量。重要的是,我们的算法避免了在每次轨迹上解决MDP的需要,使其与以前的方法比较更为实用。最后,我们用一个与AL方法来得出最差的算法。最后,我们用高的GAAL}的变式算法,我们学习了一种高的变式,我们用GAALLALALLA。