Subtrajectory Clustering: Finding Set Covers for Set Systems of Subcurves

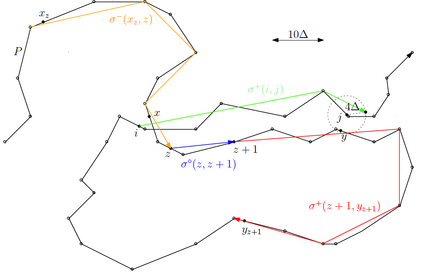
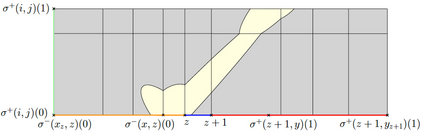
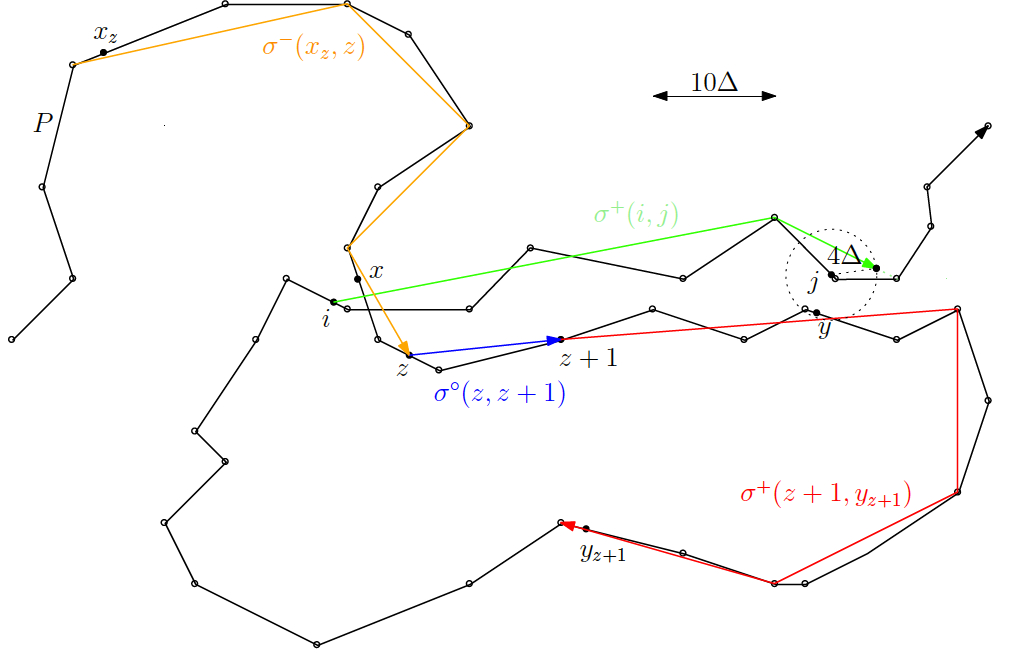
We study subtrajectory clustering under the Fr\'echet distance. Given one or more trajectories, the task is to split the trajectories into several parts, such that the parts have a good clustering structure. We approach this problem via a new set cover formulation, which we think provides a natural formalization of the problem as it is studied in many applications. Given a polygonal curve $P$ with $n$ vertices in fixed dimension, integers $k$, $\ell \geq 1$, and a real value $\Delta > 0$, the goal is to find $k$ center curves of complexity at most $\ell$ such that every point on $P$ is covered by a subtrajectory that has small Fr\'echet distance to one of the $k$ center curves ($\leq \Delta$). In many application scenarios, one is interested in finding clusters of small complexity, which is controlled by the parameter $\ell$. Our main result is a tri-criterial approximation algorithm: if there exists a solution for given parameters $k$, $\ell$, and $\Delta$, then our algorithm finds a set of $k'$ center curves of complexity at most $\ell'$ with covering radius $\Delta'$ with $k' \in O( k \ell^2 \log (k \ell))$, $\ell'\leq 2\ell$, and $\Delta'\leq 19 \Delta$. Moreover, within these approximation bounds, we can minimize $k$ while keeping the other parameters fixed. If $\ell$ is a constant independent of $n$, then, the approximation factor for the number of clusters $k$ is $O(\log k)$ and the approximation factor for the radius $\Delta$ is constant. In this case, the algorithm has expected running time in $ \tilde{O}\left( k m^2 + mn\right)$ and uses space in $O(n+m)$, where $m=\lceil\frac{L}{\Delta}\rceil$ and $L$ is the total arclength of the curve $P$. For the important case of clustering with line segments ($\ell$=2) we obtain bi-criteria approximation algorithms, where the approximation criteria are the number of clusters and the radius of the clustering.