Error analysis for local coarsening in univariate spline spaces

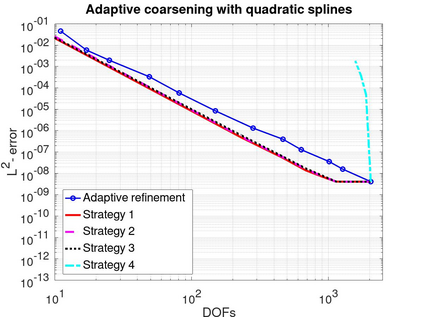
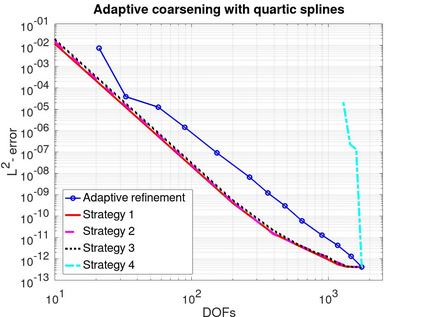
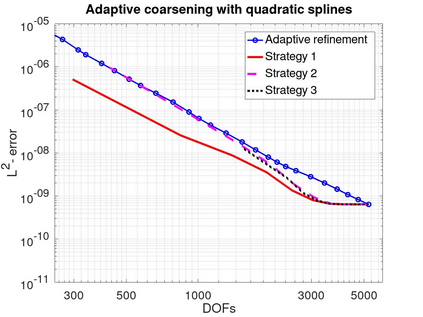
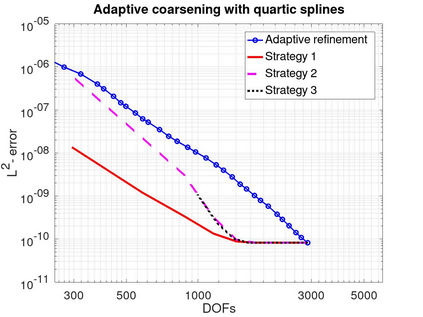
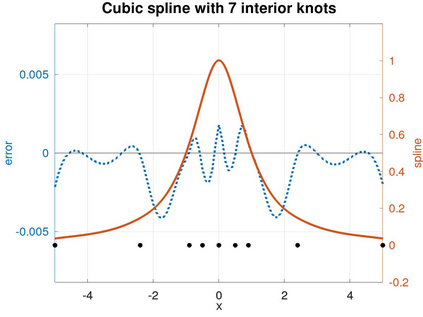
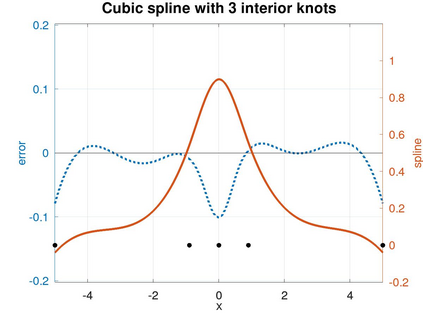
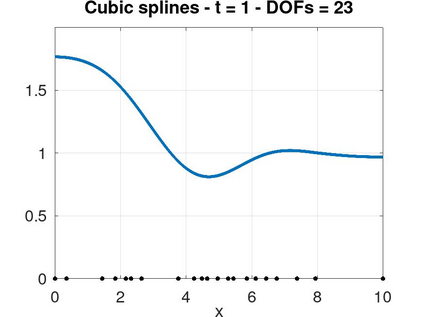
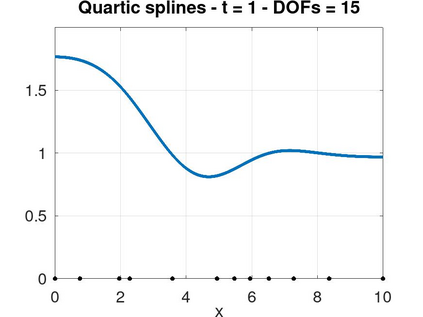
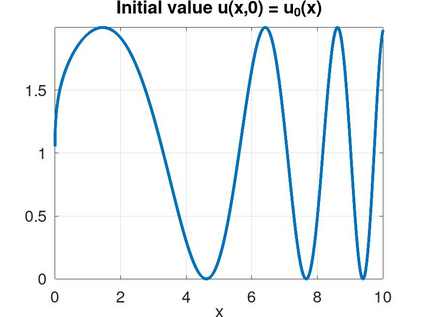
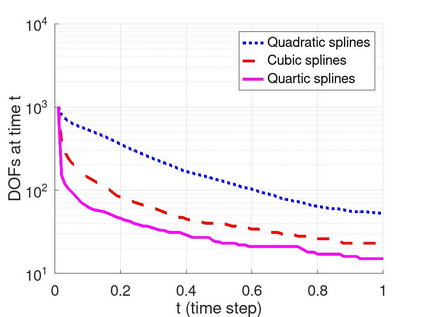
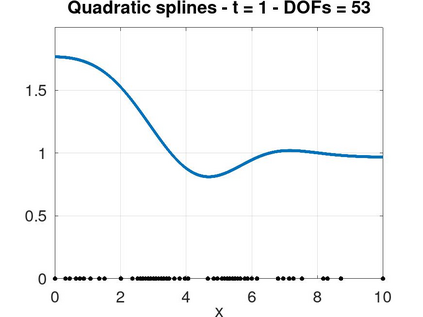
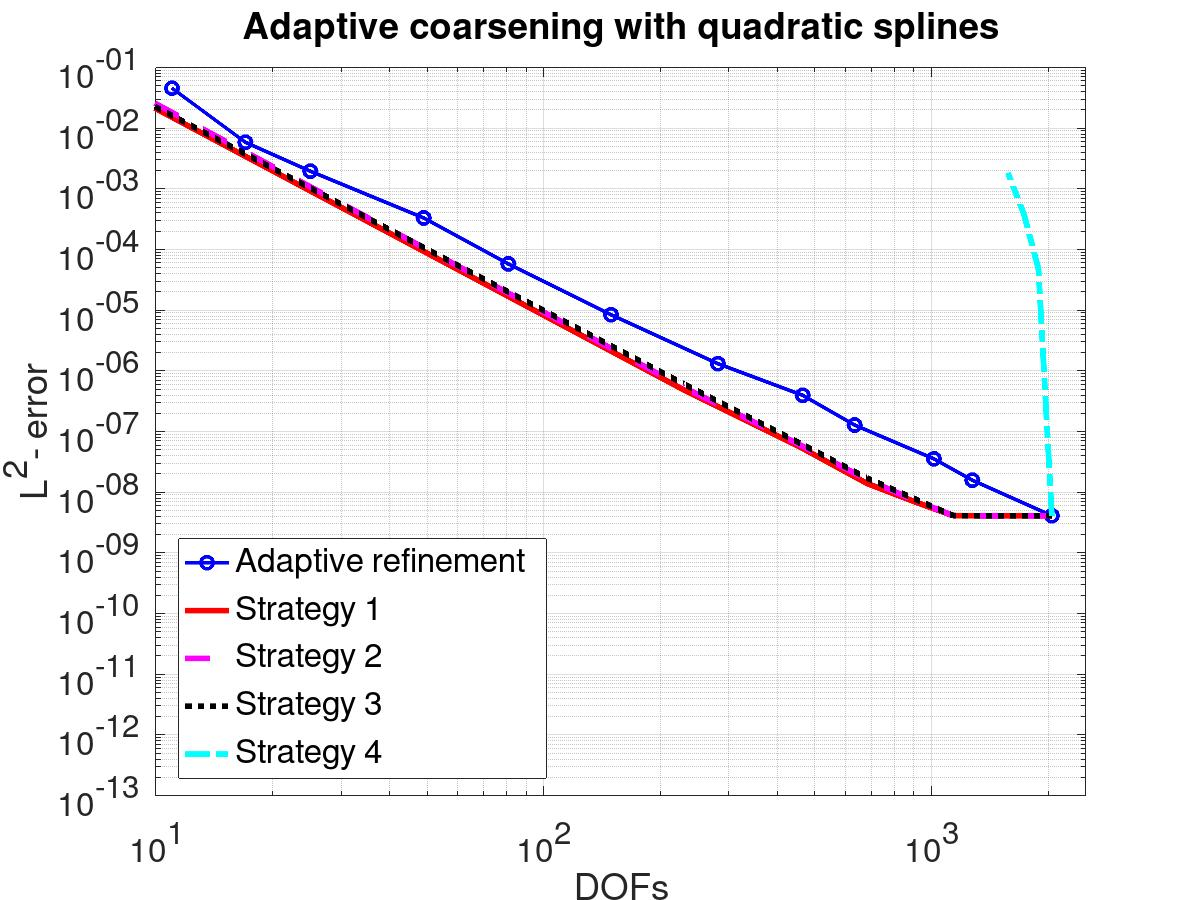
In this article we analyze the error produced by the removal of an arbitrary knot from a spline function. When a knot has multiplicity greater than one, this implies a reduction of its multiplicity by one unit. In particular, we deduce a very simple formula to compute the error in terms of some neighboring knots and a few control points of the considered spline. Furthermore, we show precisely how this error is related to the jump of a derivative of the spline at the knot. We then use the developed theory to propose efficient and very low-cost local error indicators and adaptive coarsening algorithms. Finally, we present some numerical experiments to illustrate their performance and show some applications.