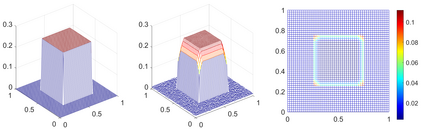
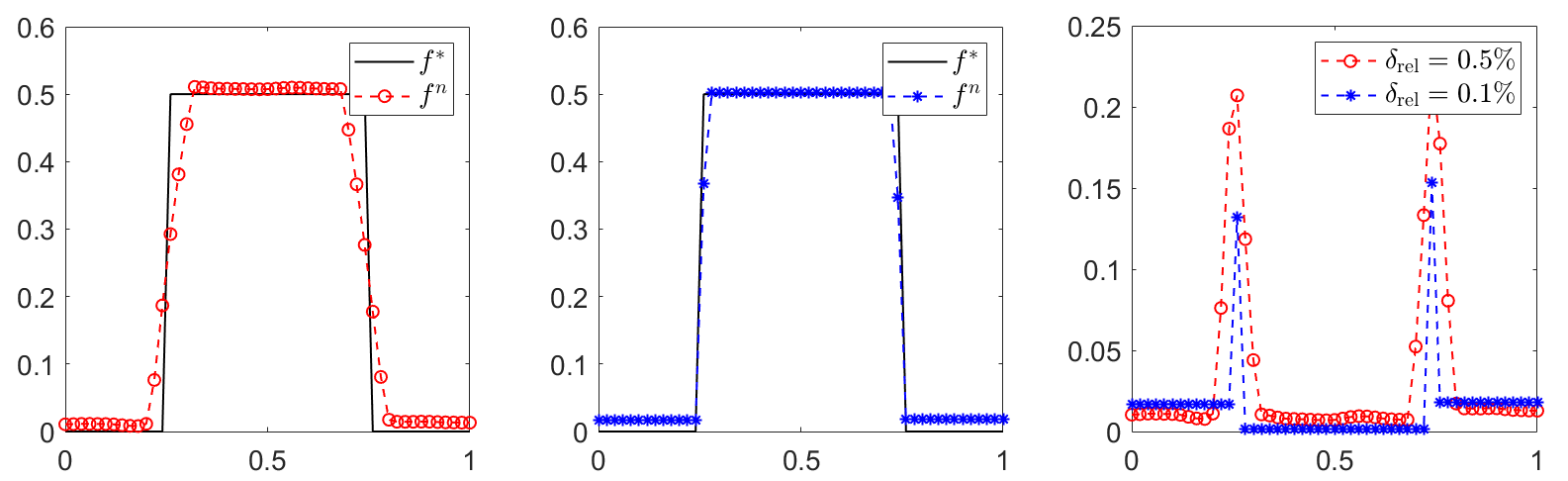
In this paper, we consider an inverse space-dependent source problem for a time-fractional diffusion equation. To deal with the ill-posedness of the problem, we transform the problem into an optimal control problem with total variational (TV) regularization. In contrast to the classical Tikhonov model incorporating $L^2$ penalty terms, the inclusion of a TV term proves advantageous in reconstructing solutions that exhibit discontinuities or piecewise constancy. The control problem is approximated by a fully discrete scheme, and convergence results are provided within this framework. Furthermore, a lineraed primal-dual iterative algorithm is proposed to solve the discrete control model based on an equivalent saddle-point reformulation, and several numerical experiments are presented to demonstrate the efficiency of the algorithm.
翻译:暂无翻译