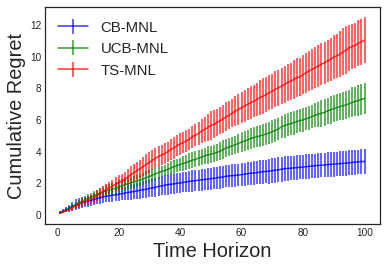
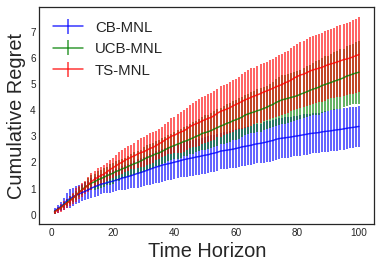
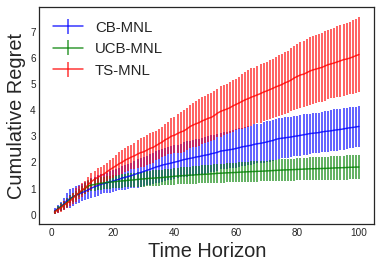
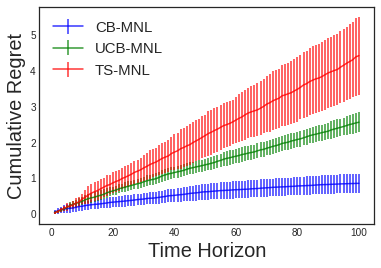
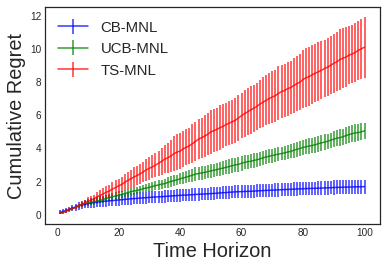
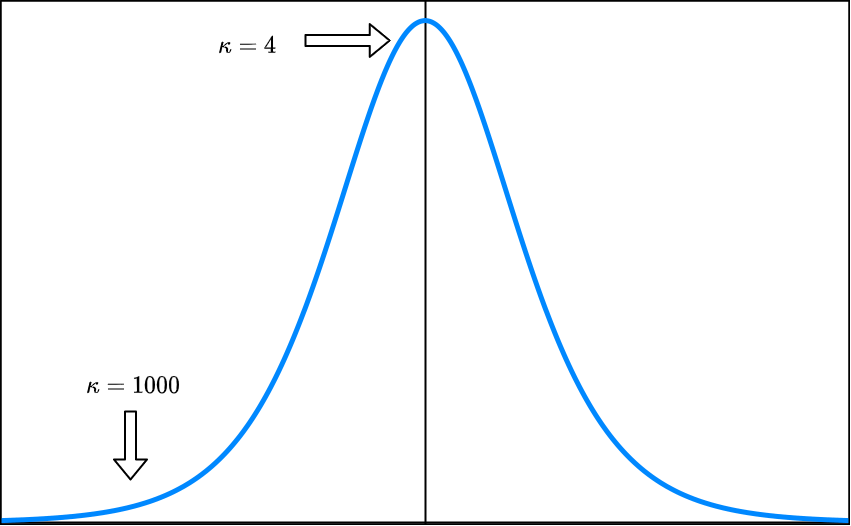
In this paper, we consider the contextual variant of the MNL-Bandit problem. More specifically, we consider a dynamic set optimization problem, where a decision-maker offers a subset (assortment) of products to a consumer and observes the response in every round. Consumers purchase products to maximize their utility. We assume that a set of attributes describe the products, and the mean utility of a product is linear in the values of these attributes. We model consumer choice behavior using the widely used Multinomial Logit (MNL) model and consider the decision maker problem of dynamically learning the model parameters while optimizing cumulative revenue over the selling horizon $T$. Though this problem has attracted considerable attention in recent times, many existing methods often involve solving an intractable non-convex optimization problem. Their theoretical performance guarantees depend on a problem-dependent parameter which could be prohibitively large. In particular, existing algorithms for this problem have regret bounded by $O(\sqrt{\kappa d T})$, where $\kappa$ is a problem-dependent constant that can have an exponential dependency on the number of attributes. In this paper, we propose an optimistic algorithm and show that the regret is bounded by $O(\sqrt{dT} + \kappa)$, significantly improving the performance over existing methods. Further, we propose a convex relaxation of the optimization step, which allows for tractable decision-making while retaining the favourable regret guarantee.
翻译:在本文中,我们考虑MNL-Bandit问题的情境变量。更具体地,我们考虑一个动态集优化问题,其中决策者向消费者提供一组产品,并在每个回合观察响应。消费者购买产品以最大化其效用。我们假设一组属性描述了产品,并且产品的平均效用在这些属性的值中是线性的。我们使用广泛使用的多项式Logit(MNL)模型来建模消费者的选择行为,并考虑在优化销售时间为$T$的累积收入时动态学习模型参数的决策者问题。虽然这个问题最近引起了相当多的关注,但许多现有方法往往涉及解决一个难以处理的非凸优化问题。它们的理论性能保证依赖于一个可能非常大的与问题相关的参数。特别地,现有算法的遗憾被限制在$O(\sqrt{\kappa d T})$,其中$\kappa$是可能具有指数依赖于属性数量的问题相关常数。在本文中,我们提出了一种乐观算法,并证明遗憾被限制在$O(\sqrt{dT}+\kappa)$,显着提高了现有方法的性能。此外,我们提出了一种优化步骤的凸松弛,它允许易处理的决策制定,同时保留了有利的遗憾保证。