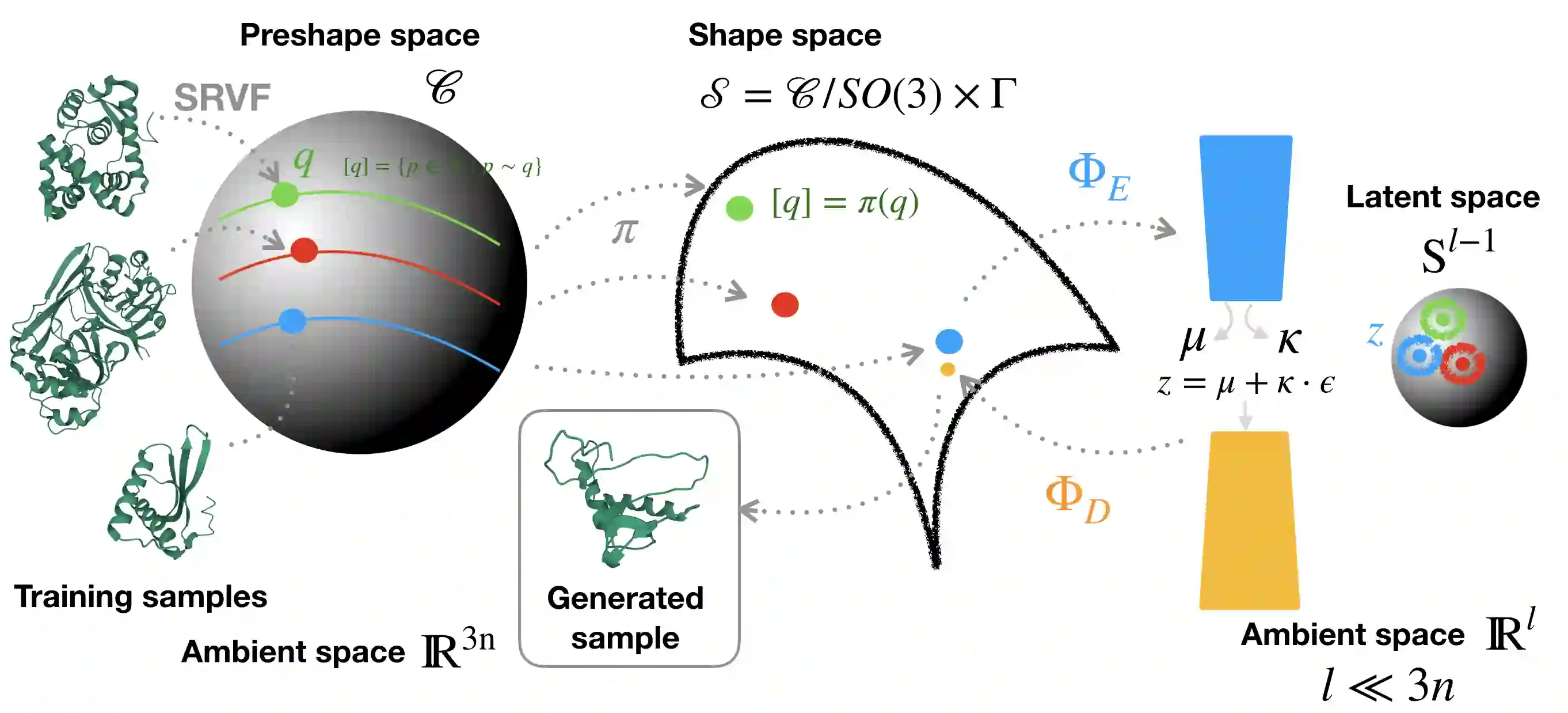
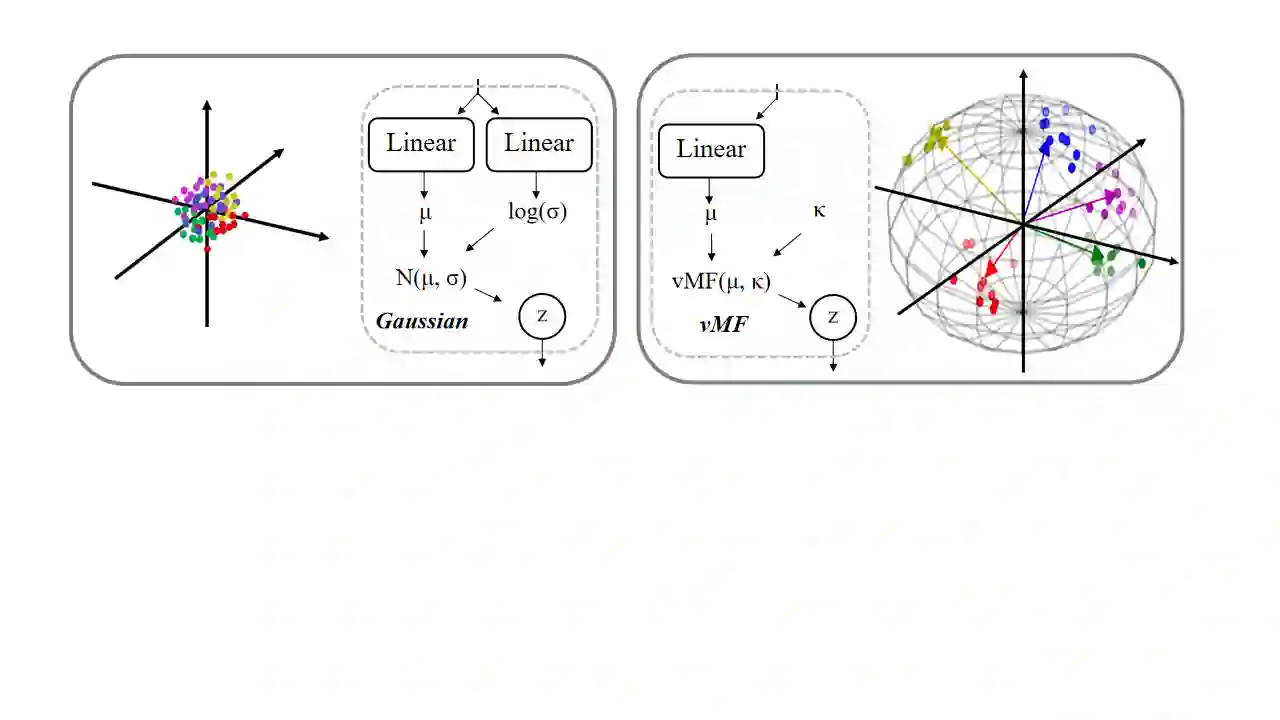
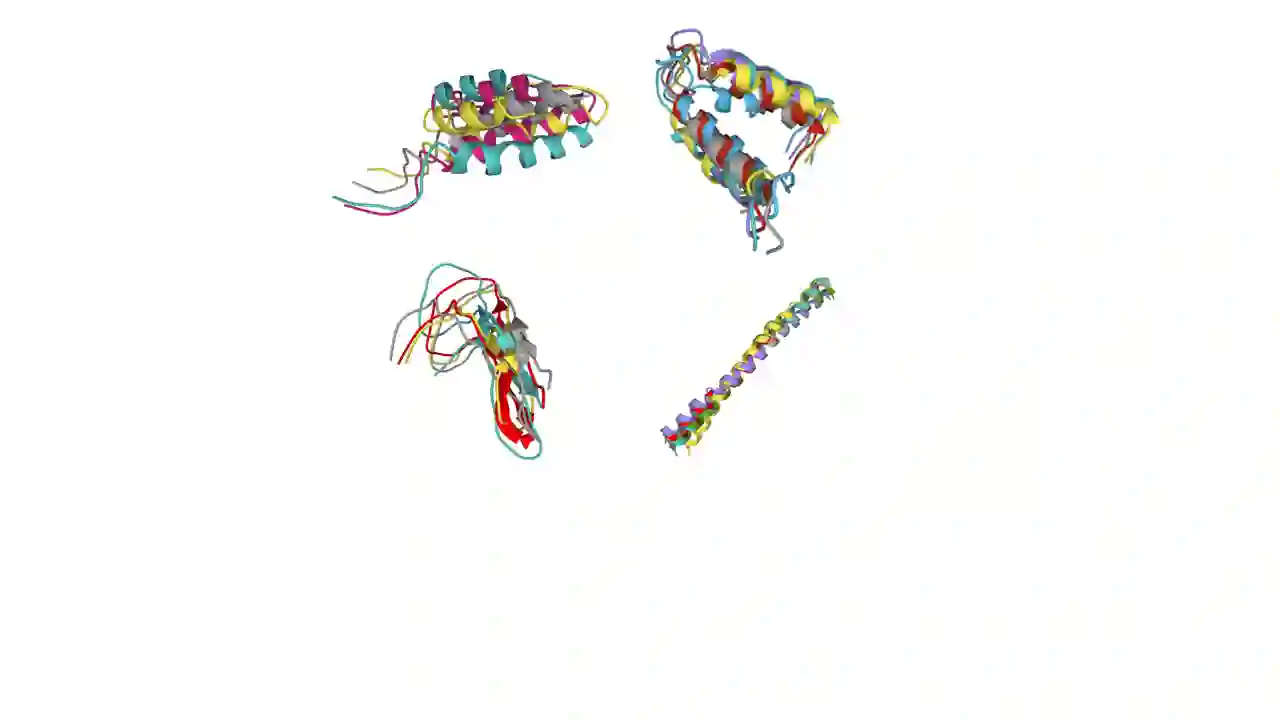
Analyzing the structure of proteins is a key part of understanding their functions and thus their role in biology at the molecular level. In addition, design new proteins in a methodical way is a major engineering challenge. In this work, we introduce a joint geometric-neural networks approach for comparing, deforming and generating 3D protein structures. Viewing protein structures as 3D open curves, we adopt the Square Root Velocity Function (SRVF) representation and leverage its suitable geometric properties along with Deep Residual Networks (ResNets) for a joint registration and comparison. Our ResNets handle better large protein deformations while being more computationally efficient. On top of the mathematical framework, we further design a Geometric Variational Auto-Encoder (G-VAE), that once trained, maps original, previously unseen structures, into a low-dimensional (latent) hyper-sphere. Motivated by the spherical structure of the pre-shape space, we naturally adopt the von Mises-Fisher (vMF) distribution to model our hidden variables. We test the effectiveness of our models by generating novel protein structures and predicting completions of corrupted protein structures. Experimental results show that our method is able to generate plausible structures, different from the structures in the training data.
翻译:分析蛋白质结构是了解蛋白质在分子层面的功能和作用的关键部分。 此外,以有条不紊的方式设计新的蛋白质是一项重大的工程挑战。 在这项工作中,我们引入了用于比较、变形和生成3D蛋白结构的几何神经网络联合方法。将蛋白质结构作为3D开放曲线来看待,我们采用广场根速度函数(SRVF)代表制,并将其合适的几何特性与深层残余网络(ResNets)一起用于联合注册和比较。我们的ResNet(ResNets)处理更好的大型蛋白质变形,同时提高计算效率。在数学框架之外,我们进一步设计了一种几何测量动自动电解变网络(G-VAE),一旦经过培训,将原始的、先前看不见的结构映射为低维(相对隐蔽的)超光谱。我们自然采用了冯米斯-Fisher(vMF)的分布来模拟我们隐藏的变量。我们测试了数学结构的有效性,我们从新的蛋白质结构中得出了可靠的实验性模型,我们通过生成的模型的模型的模型的模型的模型的模型将产生可靠的分析结果,以预测结果,以显示我们的蛋白质结构。