Combining Sobolev Smoothing with Parameterized Shape Optimization

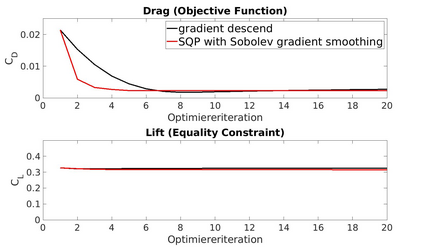
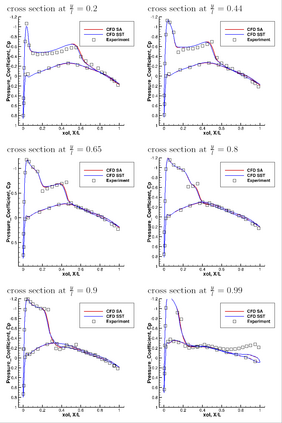
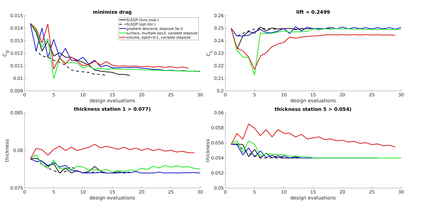
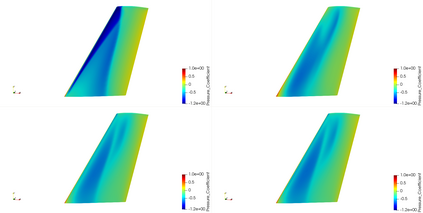
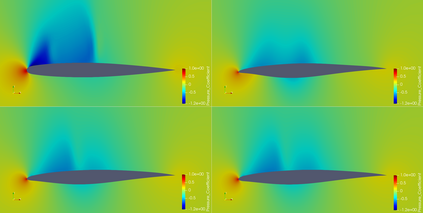
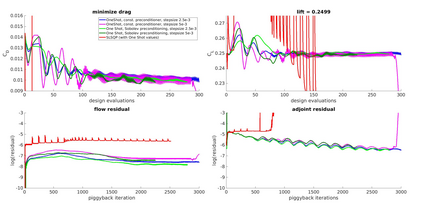
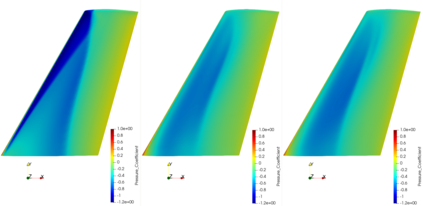
On the one hand Sobolev gradient smoothing can considerably improve the performance of aerodynamic shape optimization and prevent issues with regularity. On the other hand Sobolev smoothing can also be interpreted as an approximation for the shape Hessian. This paper demonstrates, how Sobolev smoothing, interpreted as a shape Hessian approximation, offers considerable benefits, although the parameterization is smooth in itself already. Such an approach is especially beneficially in the context of simultaneous analysis and design, where we deal with inexact flow and adjoint solutions, also called One Shot optimization. Furthermore, the incorporation of the parameterization allows for direct application to engineering test cases, where shapes are always described by a CAD model. The new methodology presented in this paper is used for reference test cases from aerodynamic shape optimization and performance improvements in comparison to a classical Quasi-Newton scheme are shown.