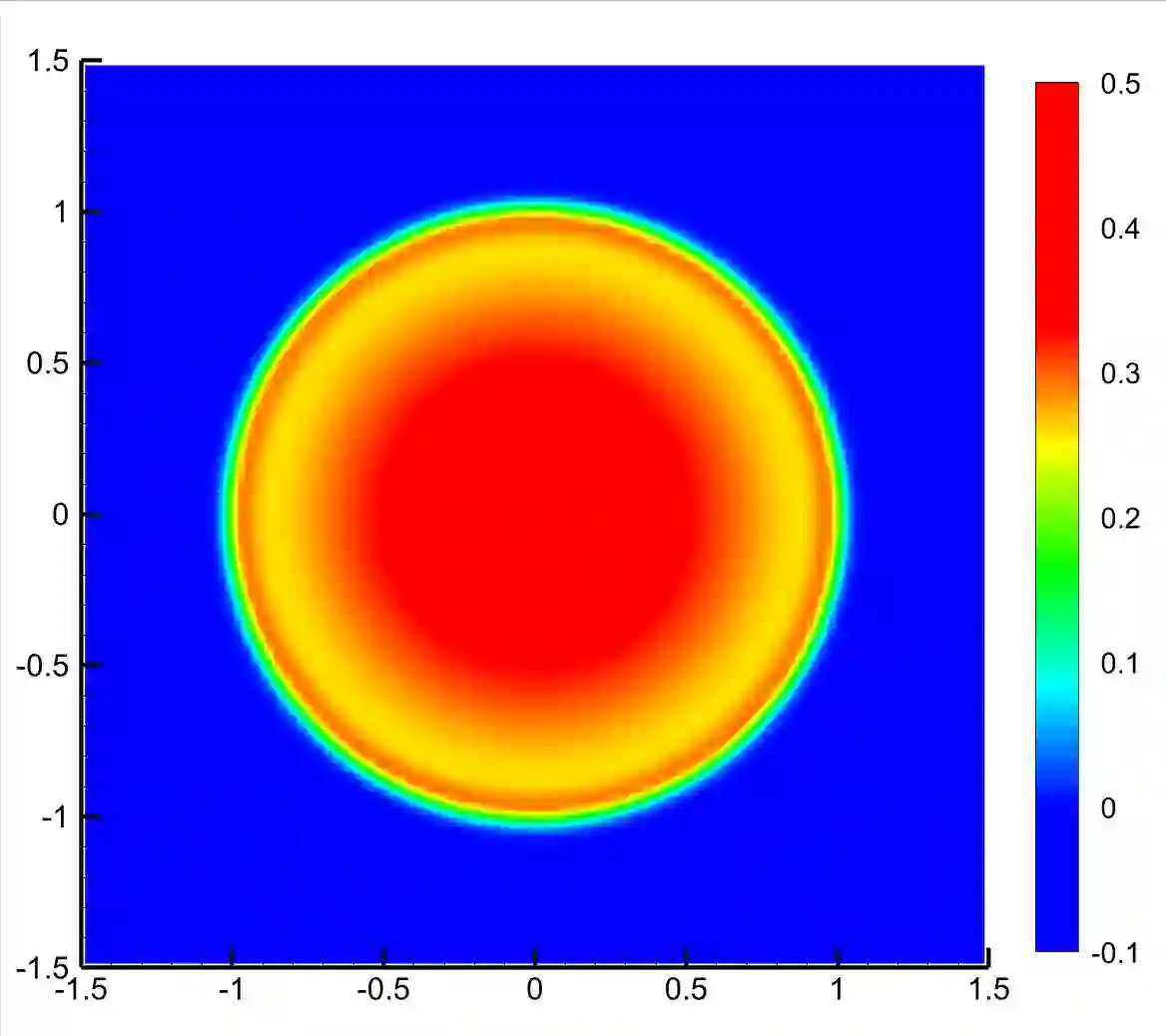
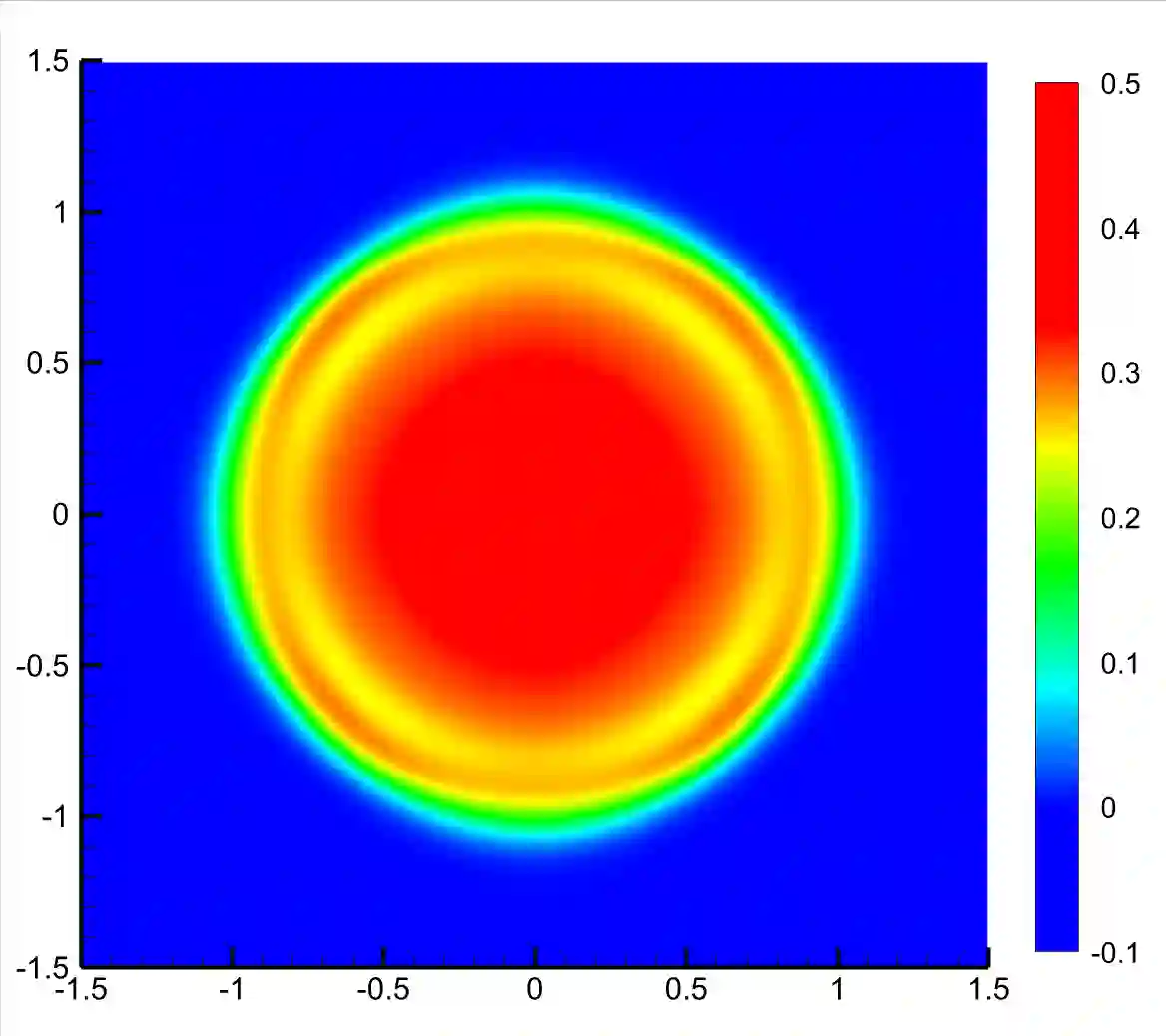
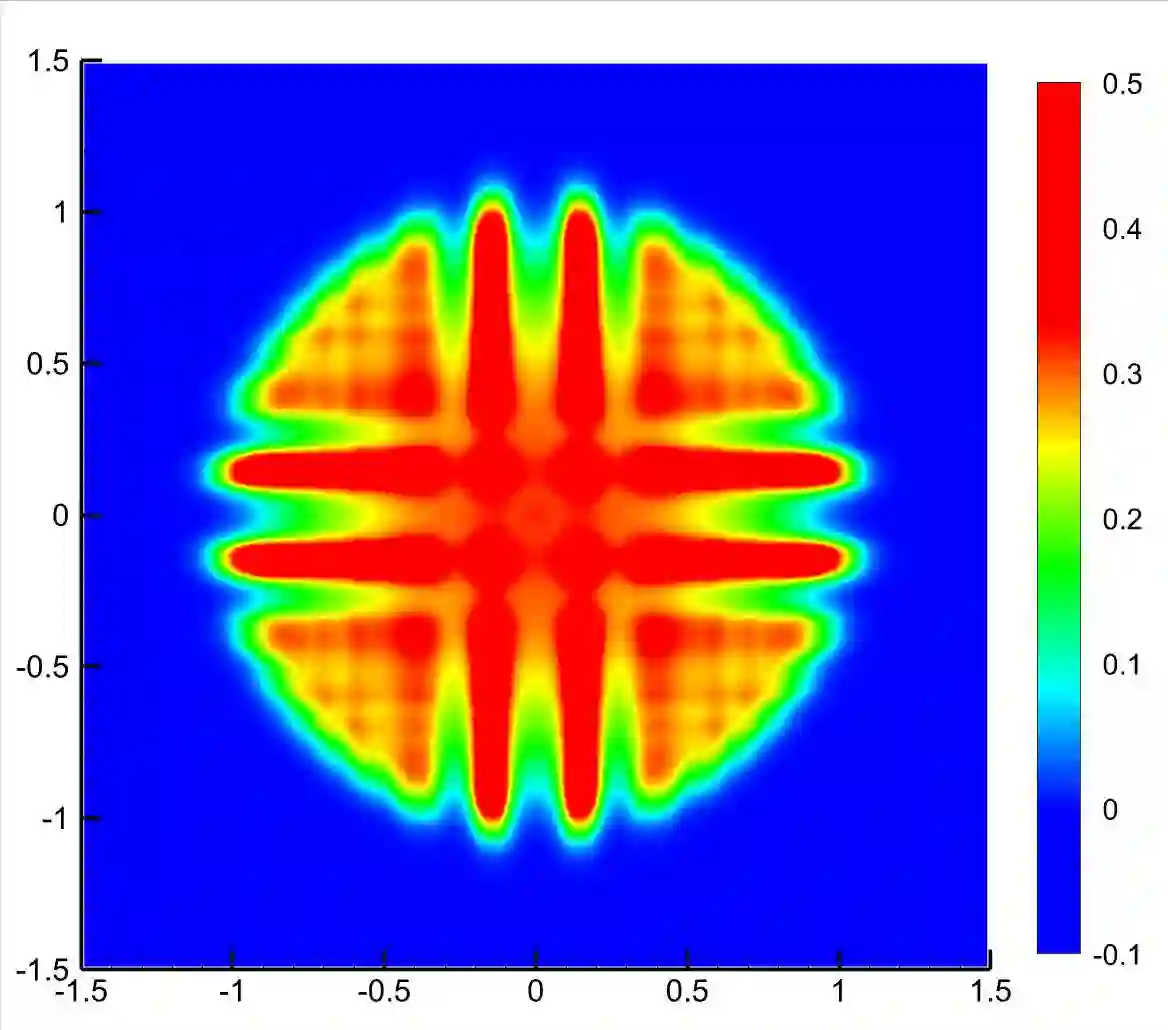
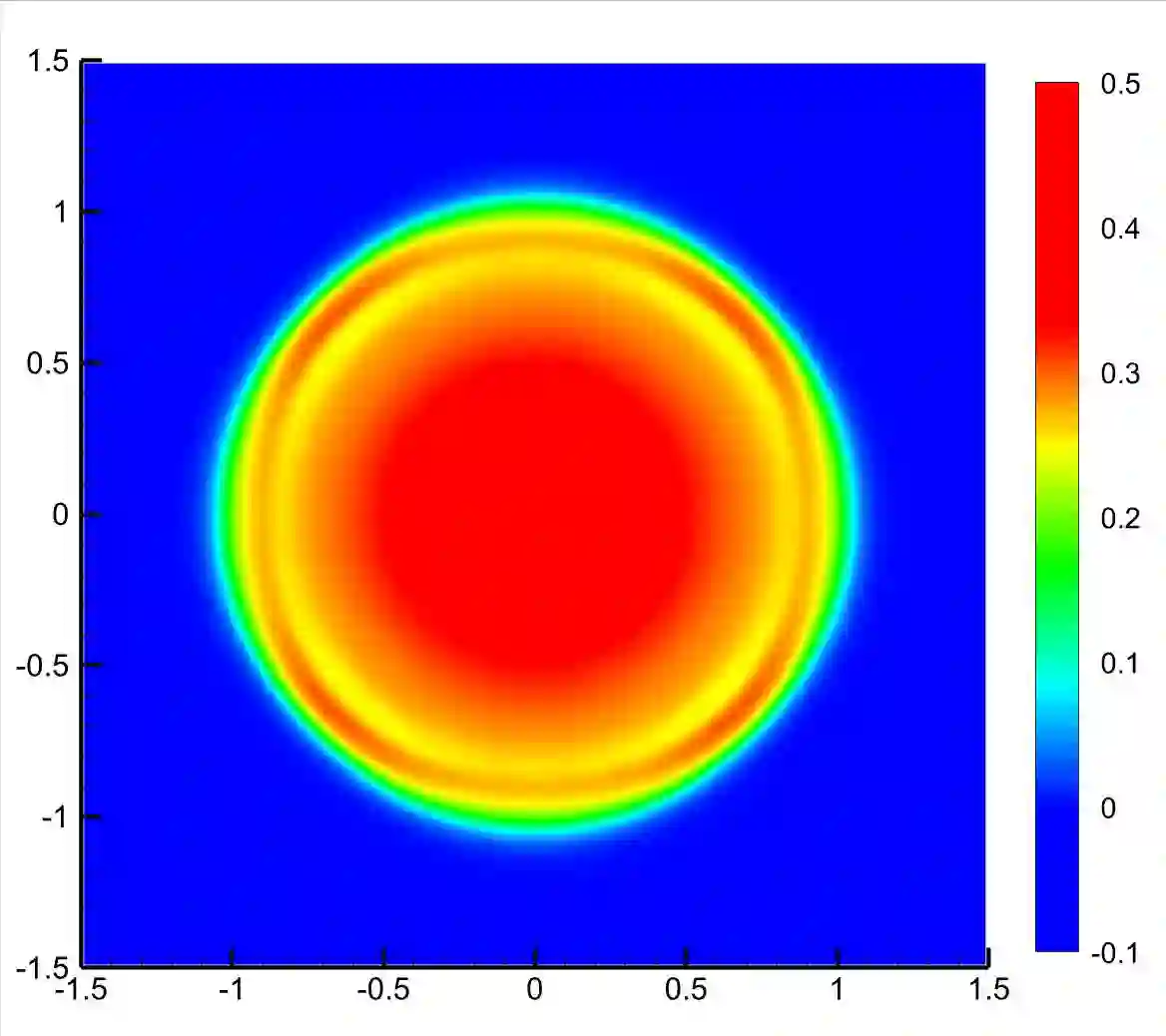
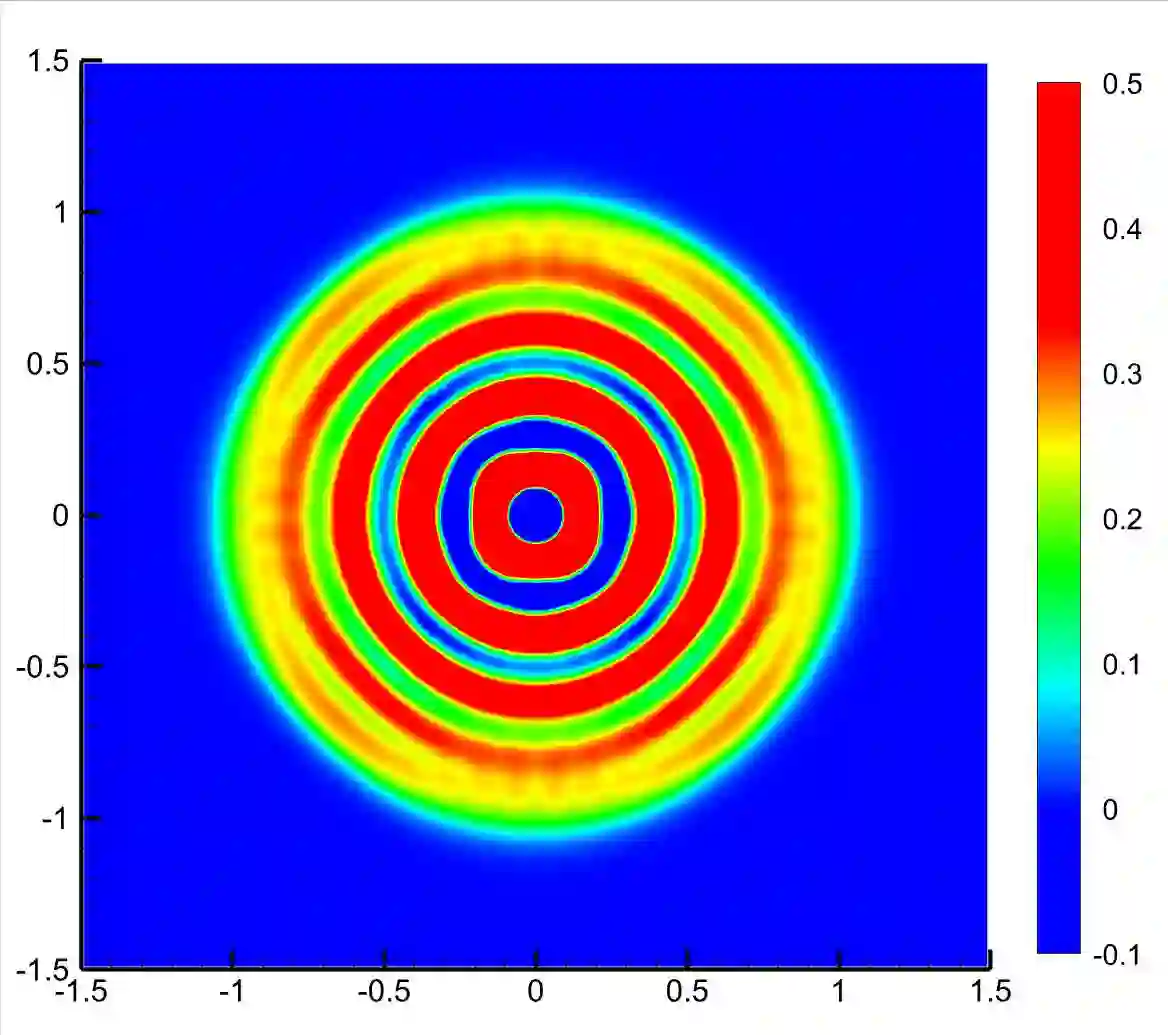
A spatial second-order scheme for the nonlinear radiative transfer equations is introduced in this paper. The discretization scheme is based on the filtered spherical harmonics ($FP_N$) method for the angular variable and the unified gas kinetic scheme (UGKS) framework for the spatial and temporal variables respectively. In order to keep the scheme positive and second-order accuracy, firstly, we use the implicit Monte Carlo linearization method [6] in the construction of the UGKS numerical boundary fluxes. Then, by carefully analyzing the constructed second-order fluxes involved in the macro-micro decomposition, which is induced by the $FP_N$ angular discretization, we establish the sufficient conditions that guarantee the positivity of the radiative energy density and material temperature. Finally, we employ linear scaling limiters for the angular variable in the $P_N$ reconstruction and for the spatial variable in the piecewise linear slopes reconstruction respectively, which are shown to be realizable and reasonable to enforce the sufficient conditions holding. Thus, the desired scheme, called the $PPFP_N$-based UGKS, is obtained. Furthermore, in the regime $\epsilon\ll 1$ and the regime $\epsilon=O(1)$, a simplified spatial second-order scheme, called the $PPFP_N$-based SUGKS, is presented, which possesses all the properties of the non-simplified one. Inheriting the merit of UGKS, the proposed schemes are asymptotic preserving. By employing the $FP_N$ method for the angular variable, the proposed schemes are almost free of ray effects. To our best knowledge, this is the first time that spatial second-order, positive, asymptotic preserving and almost free of ray effects schemes are constructed for the nonlinear radiative transfer equations without operator splitting. Various numerical experiments are included to validate the properties of the proposed schemes.
翻译:暂无翻译