Asymptotic expansions for the linear PDEs with oscillatory input terms; Analytical form and error analysis

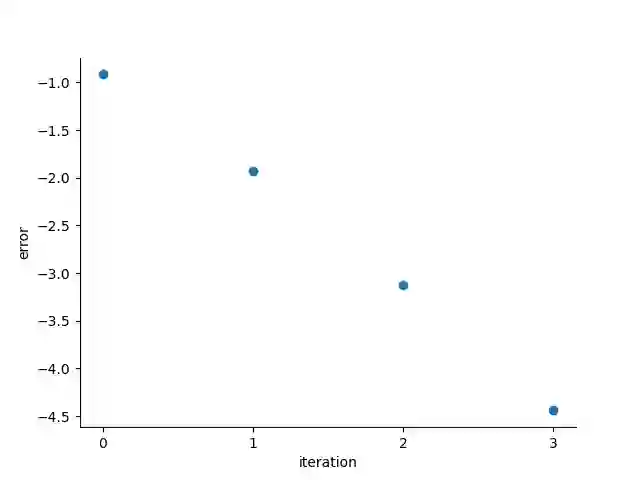
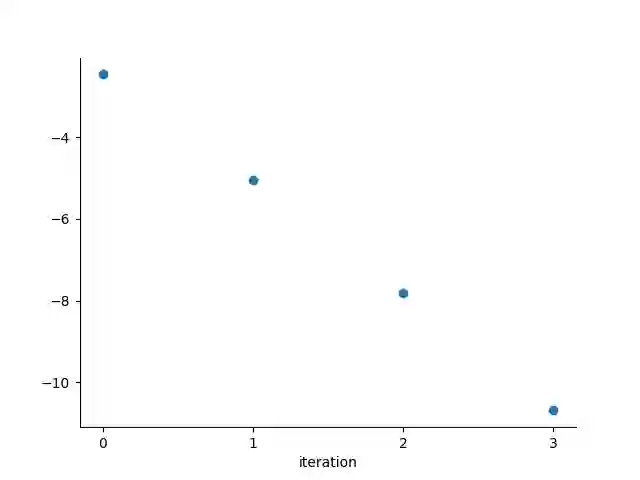
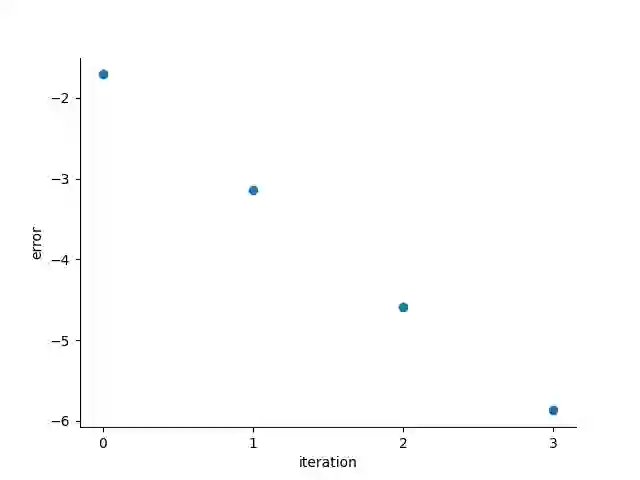
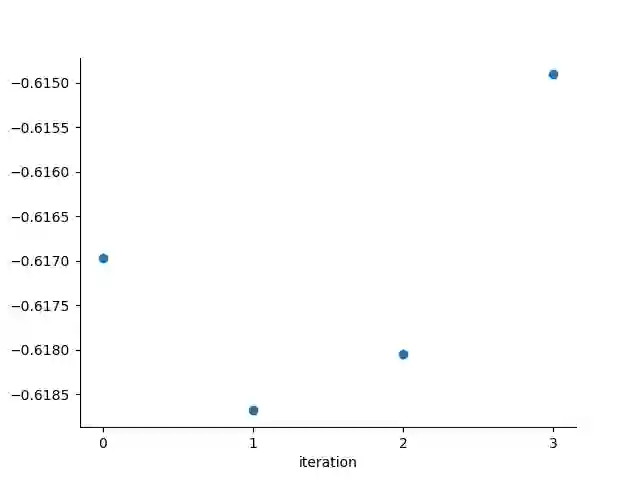
Partial differential equations with highly oscillatory input terms are hardly ever solvable analytically and their numerical treatment is difficult. Modulated Fourier expansion used as an {\it ansatz} is a well known and extensively investigated tool in asymptotic numerical approach for this kind of problems. Although the efficiency of this approach has been recognised, its error analysis has not been investigated rigorously for general forms of linear PDEs. In this paper, we start such kind of investigations for a general form of linear PDEs with an input term characterised by a single high frequency. More precisely we derive an analytical form of such an expansion and provide a formula for the error of its truncation. Theoretical investigations are illustrated by computational simulations.