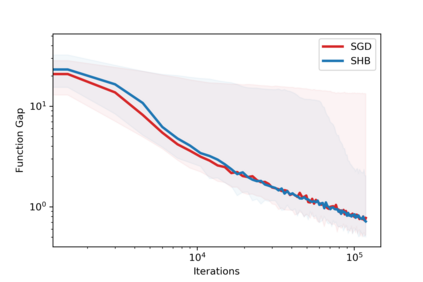
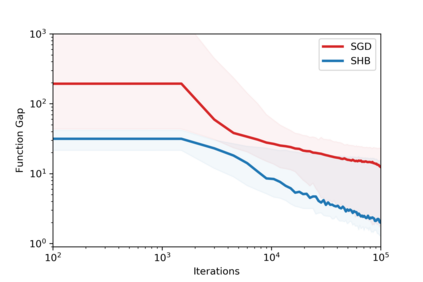
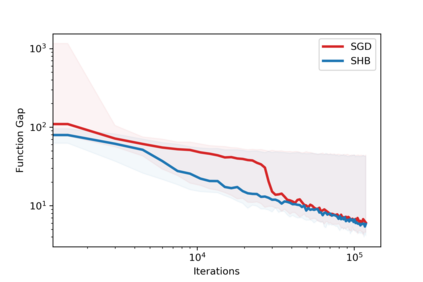
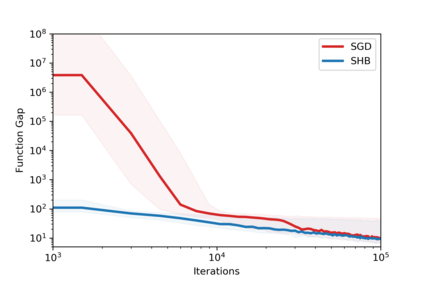
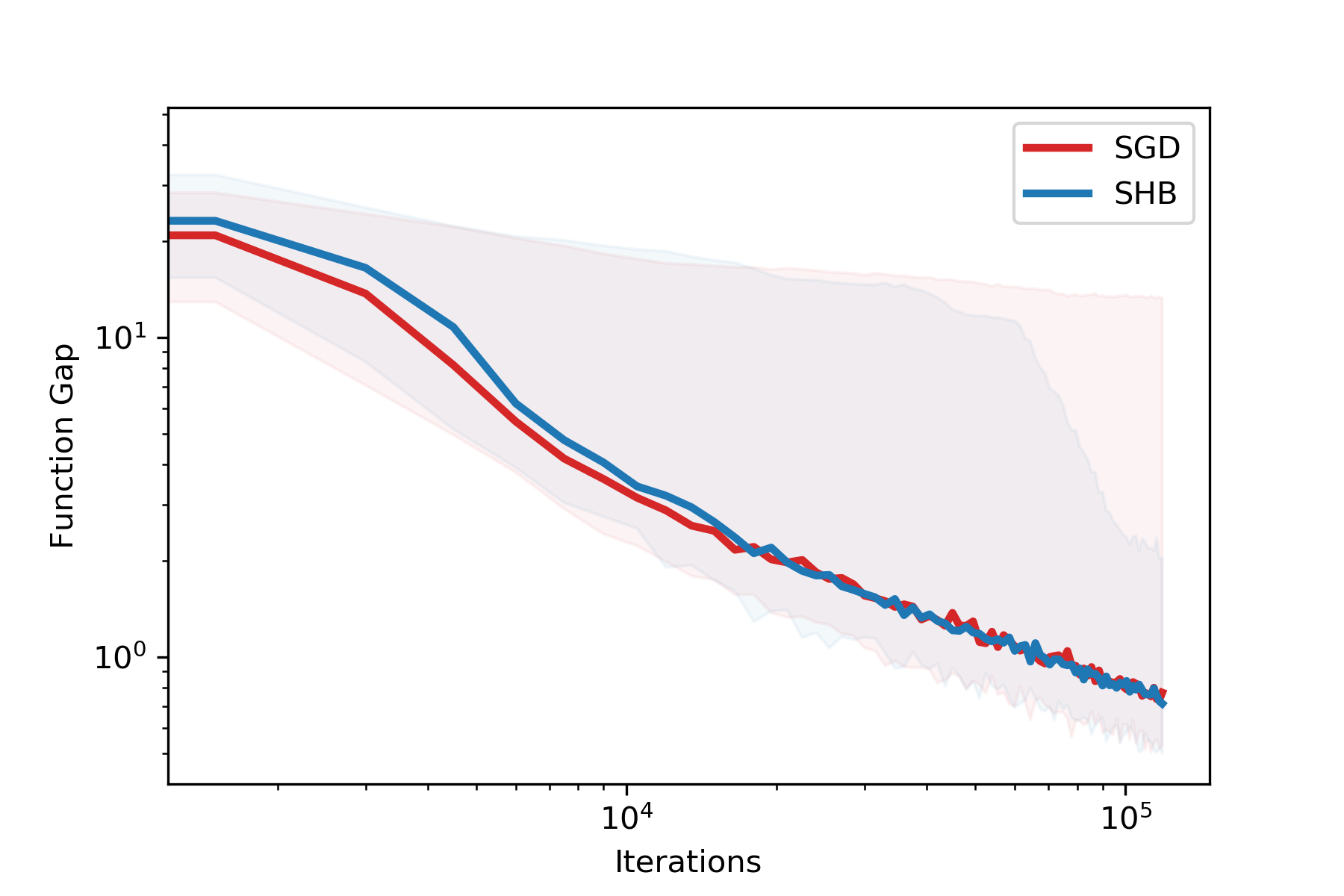
Stochastic gradient methods with momentum are widely used in applications and at the core of optimization subroutines in many popular machine learning libraries. However, their sample complexities have not been obtained for problems beyond those that are convex or smooth. This paper establishes the convergence rate of a stochastic subgradient method with a momentum term of Polyak type for a broad class of non-smooth, non-convex, and constrained optimization problems. Our key innovation is the construction of a special Lyapunov function for which the proven complexity can be achieved without any tuning of the momentum parameter. For smooth problems, we extend the known complexity bound to the constrained case and demonstrate how the unconstrained case can be analyzed under weaker assumptions than the state-of-the-art. Numerical results confirm our theoretical developments.
翻译:许多流行的机器学习图书馆在应用中和在优化子程序核心中广泛使用具有动力的沙尘梯方法,但是,对于超出软质或光滑的问题,尚未获得其样本复杂性,本文确定了一种具有动力的多孔型微粒亚梯度方法的趋同率,其动力期为一大批非软性、非软质和限制优化问题。我们的关键创新是构建一种特殊的Lyapunov功能,经过证明的复杂程度可以在不调动动力参数的情况下实现。关于顺利的问题,我们将已知的复杂程度扩大到受约束的病例,并展示如何在比目前最先进的假设更弱的假设下分析未受限制的病例。数字结果证实了我们的理论发展。