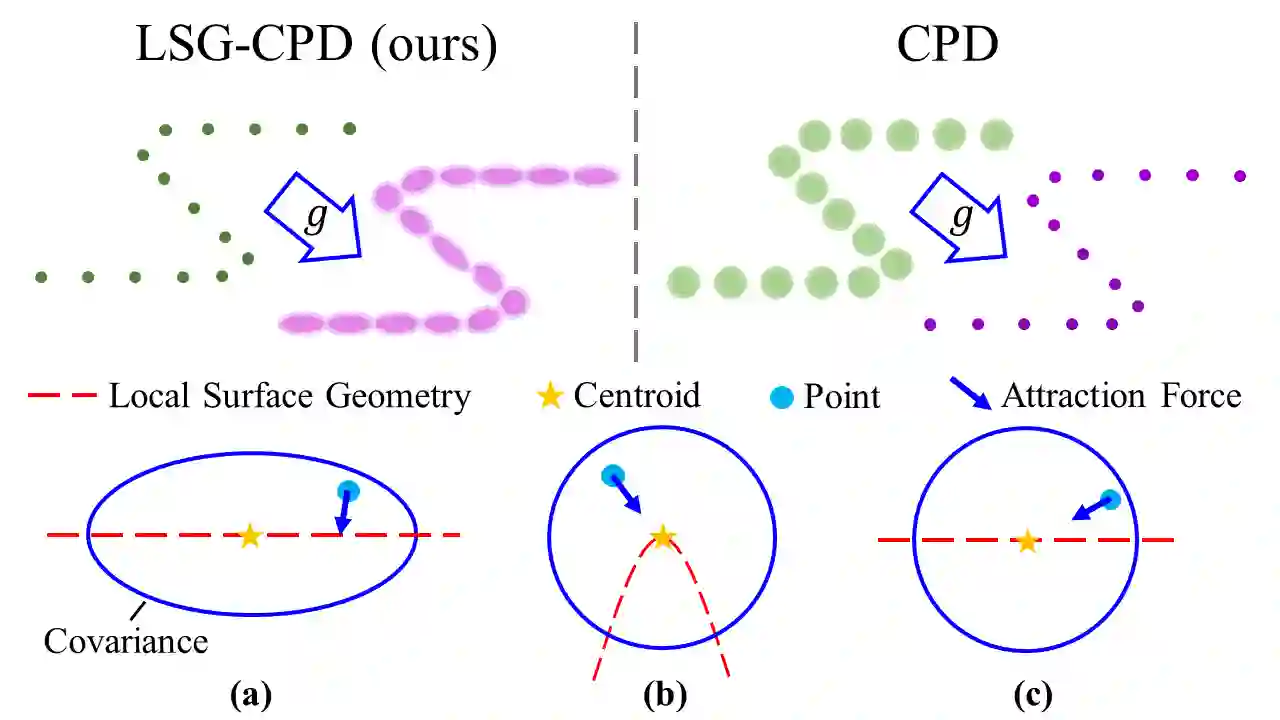
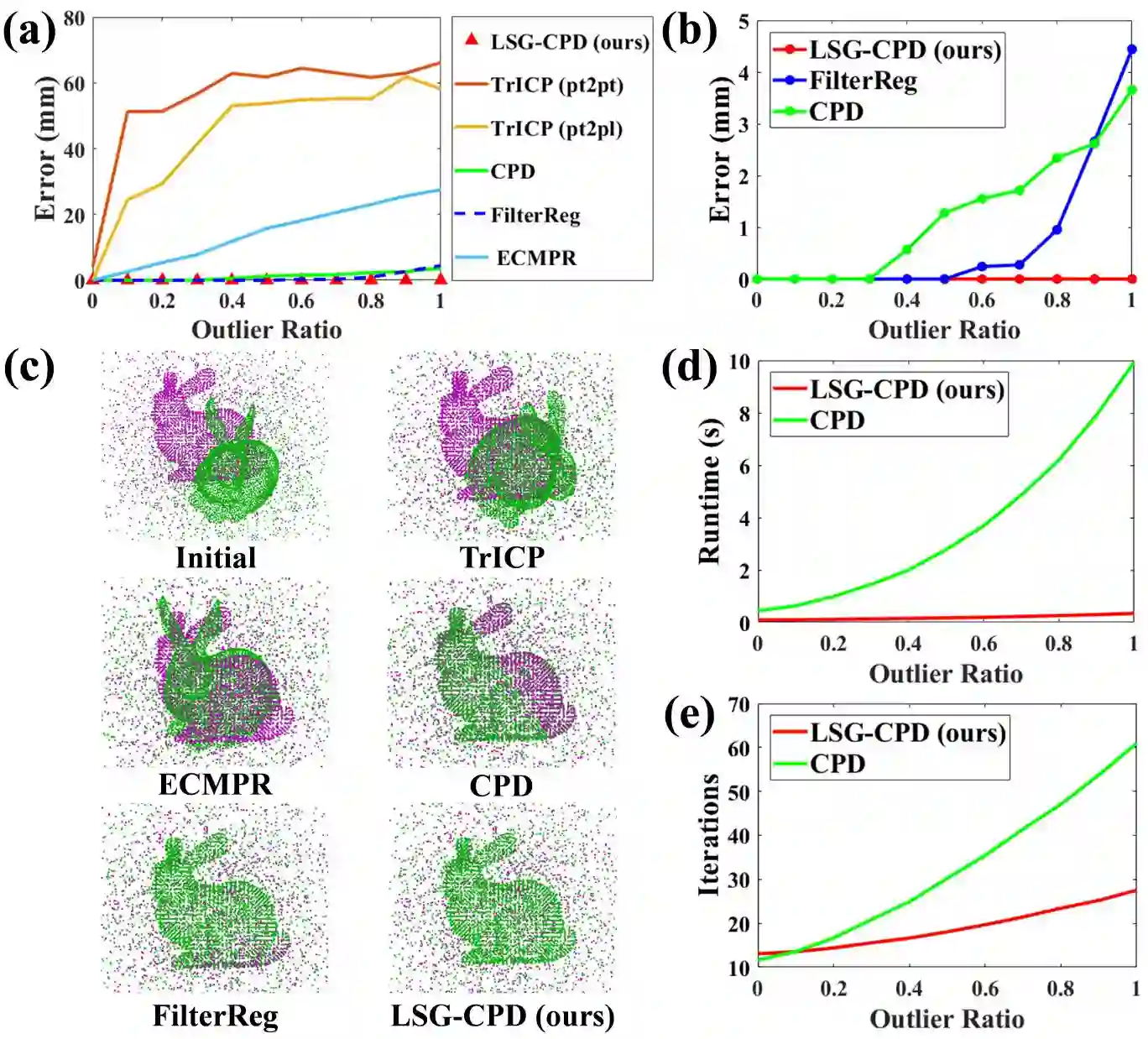
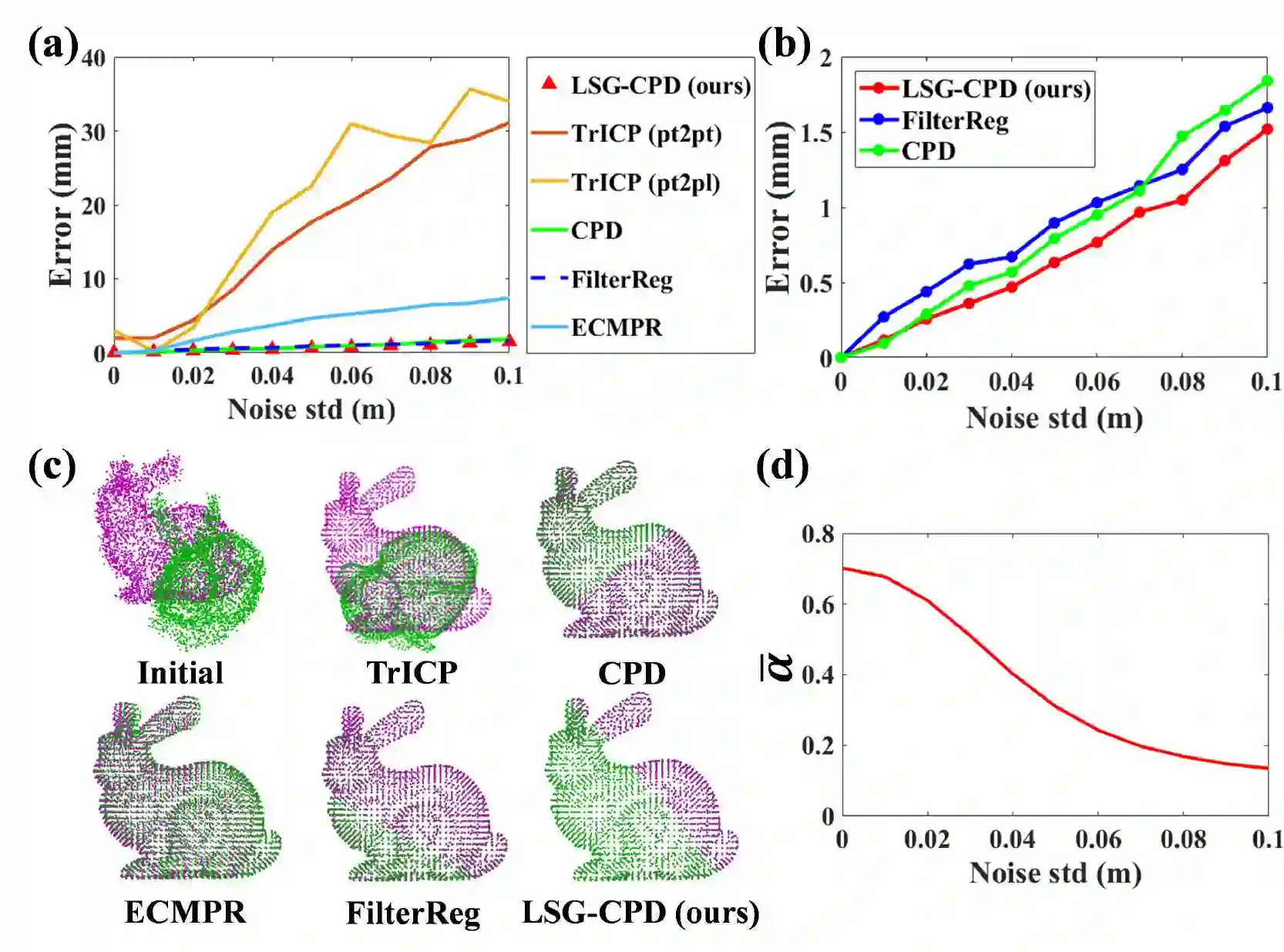
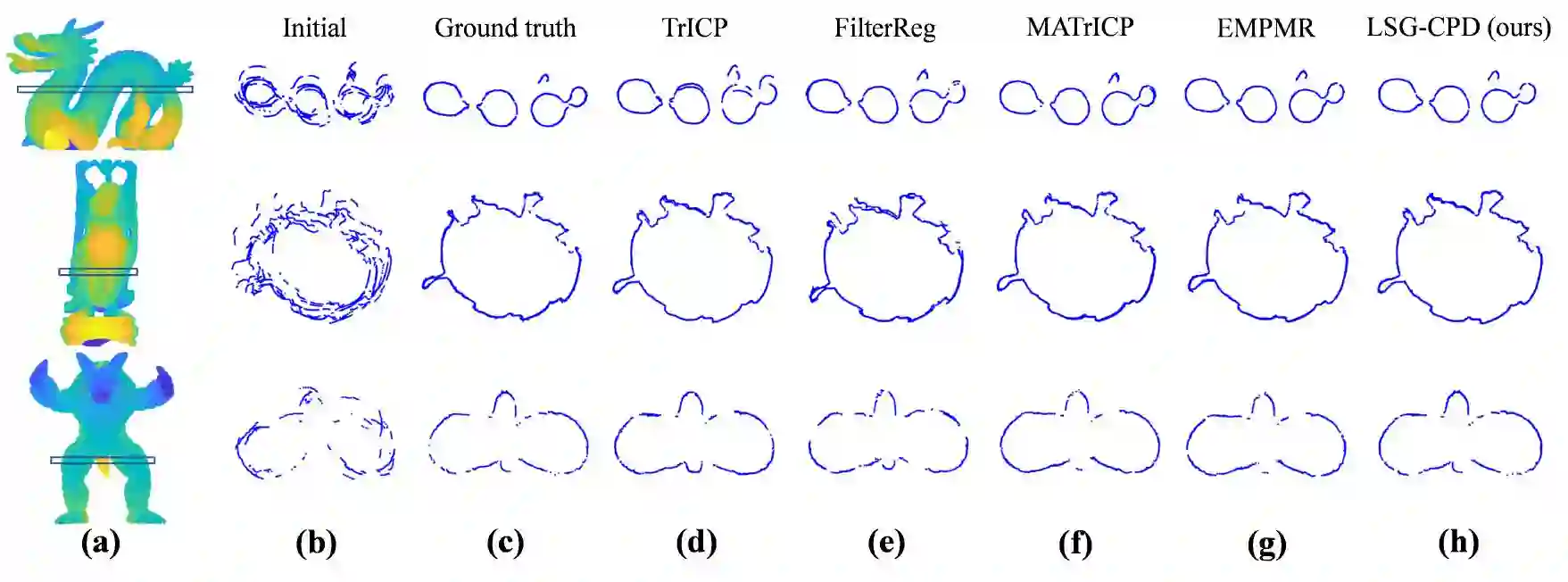
Probabilistic point cloud registration methods are becoming more popular because of their robustness. However, unlike point-to-plane variants of iterative closest point (ICP) which incorporate local surface geometric information such as surface normals, most probabilistic methods (e.g., coherent point drift (CPD)) ignore such information and build Gaussian mixture models (GMMs) with isotropic Gaussian covariances. This results in sphere-like GMM components which only penalize the point-to-point distance between the two point clouds. In this paper, we propose a novel method called CPD with Local Surface Geometry (LSG-CPD) for rigid point cloud registration. Our method adaptively adds different levels of point-to-plane penalization on top of the point-to-point penalization based on the flatness of the local surface. This results in GMM components with anisotropic covariances. We formulate point cloud registration as a maximum likelihood estimation (MLE) problem and solve it with the Expectation-Maximization (EM) algorithm. In the E step, we demonstrate that the computation can be recast into simple matrix manipulations and efficiently computed on a GPU. In the M step, we perform an unconstrained optimization on a matrix Lie group to efficiently update the rigid transformation of the registration. The proposed method outperforms state-of-the-art algorithms in terms of accuracy and robustness on various datasets captured with range scanners, RGBD cameras, and LiDARs. Also, it is significantly faster than modern implementations of CPD. The source code is available at https://github.com/ChirikjianLab/LSG-CPD.git.
翻译:概率点云的登记方法因其稳健性而越来越受欢迎。 但是,与包含地表正常度等局部表面几何信息的迭接点至平面最接近点点(ICP)变方不同的是,我们采用的方法(例如,一致点漂移(CPD))忽略了这些信息,并建立了高斯混合模型(GMMM)和异向高斯多变。这导致像球体一样的GMM组件,它只会损害两点云之间的点到点距离。在本文中,我们提出了一种叫“本地表面测深(LSG-CP) CP(LSG-CPD) ” 的新颖方法,用于硬点云登记。我们的方法在点到点的平坦度上添加了不同的点到点惩罚程度。这导致GMM组件与异质变异性。我们将点云的登记作为最大可能性估计(MLE) 问题,并用预期- 马克化(EM) 算法。 在简化的 Erational- massalal 中,我们用一个快速的进度将数据转换为GRB 。