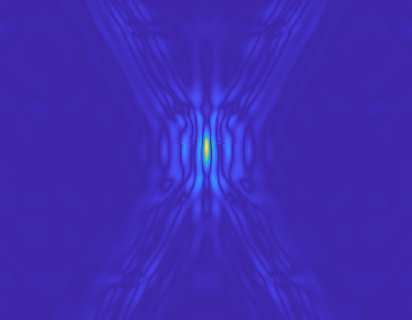
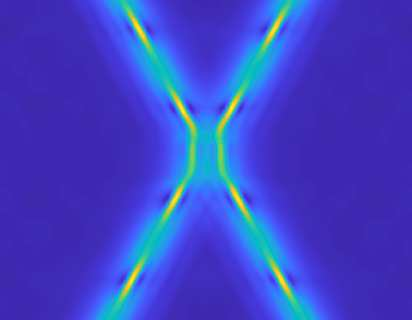
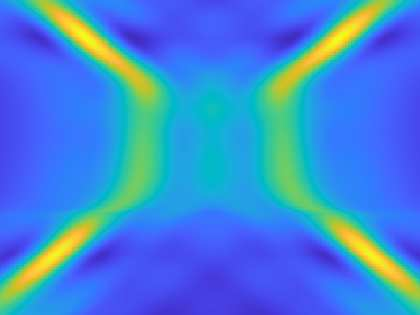
We study an optimization problem related to the approximation of given data by a linear combination of transformed modes. In the simplest case, the optimization problem reduces to a minimization problem well-studied in the context of proper orthogonal decomposition. Allowing transformed modes in the approximation renders this approach particularly useful to compress data with transported quantities, which are prevalent in many flow applications. We prove the existence of a solution to the infinite-dimensional optimization problem. Towards a numerical implementation, we compute the gradient of the cost functional and derive a suitable discretization in time and space. We demonstrate the theoretical findings with three challenging numerical examples.
翻译:我们研究的是与通过转变模式的线性组合对给定数据进行近似近似有关的优化问题。在最简单的例子中,优化问题被减为在适当的正心分解背景下经过充分研究的最小化问题。允许近似中的变化模式使得这一方法特别有助于用许多流动应用中普遍存在的运输量压缩数据。我们证明存在着解决无限维化优化问题的办法。在数字执行中,我们计算成本功能的梯度,并得出在时间和空间上适当的离散。我们用三个具有挑战性的数字例子来展示理论结论。