A high order unfitted hybridizable discontinuous Galerkin method for linear elasticity

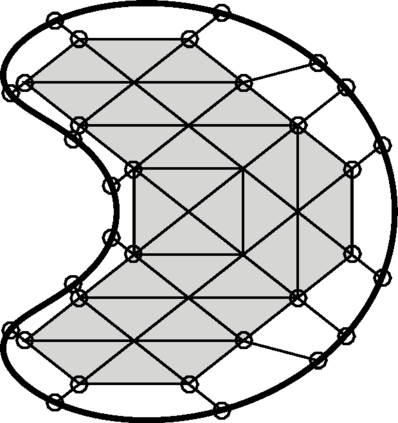
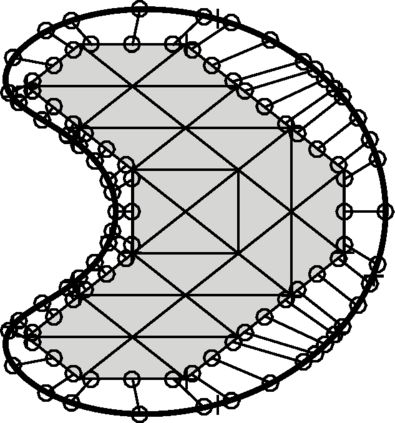
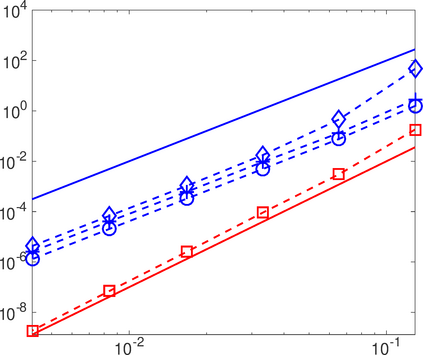
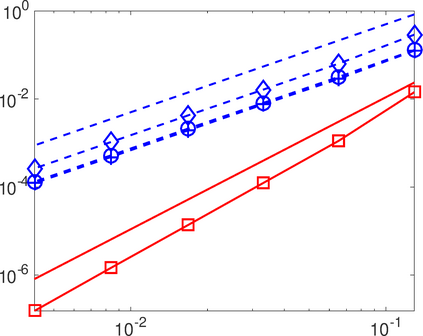
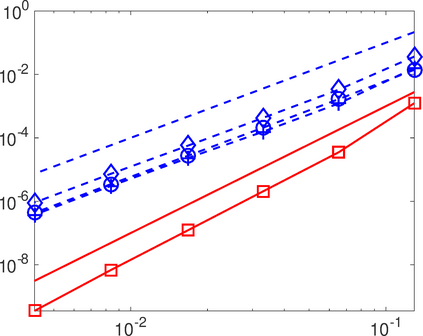
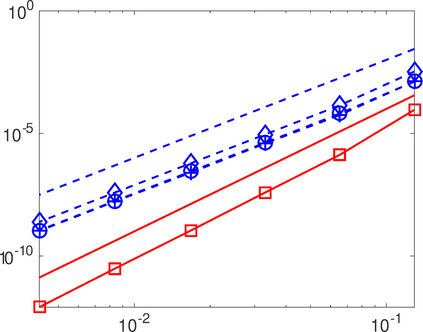
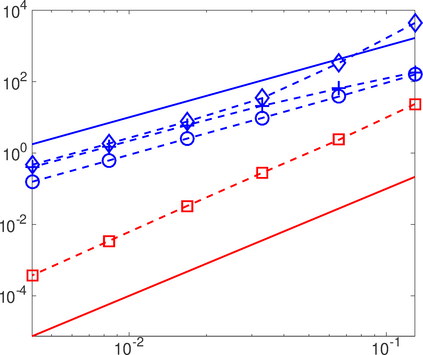
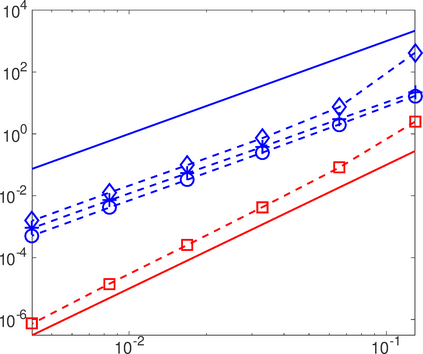
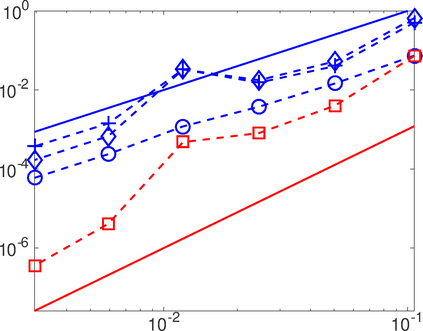
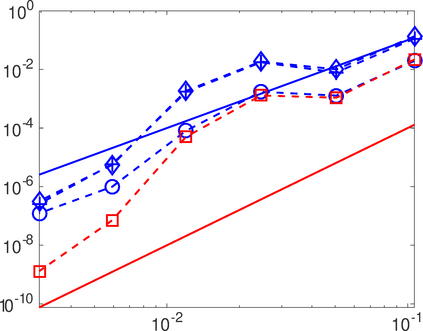
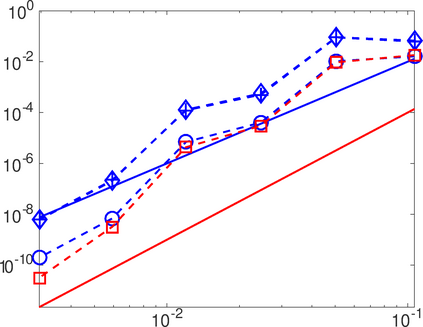
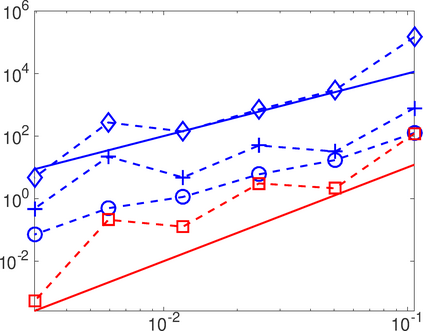
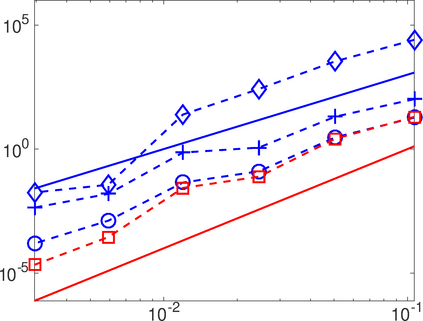
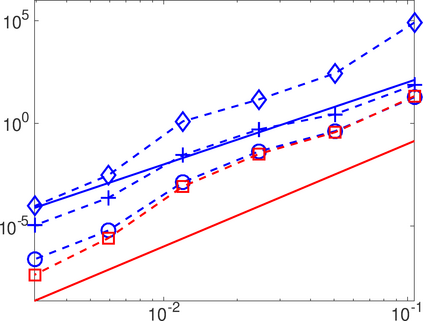
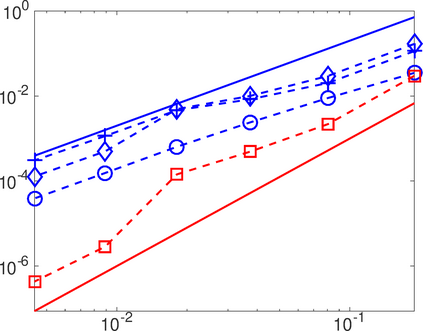
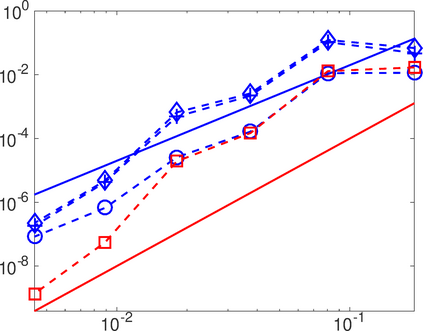
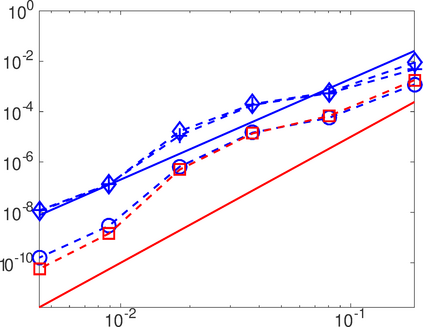
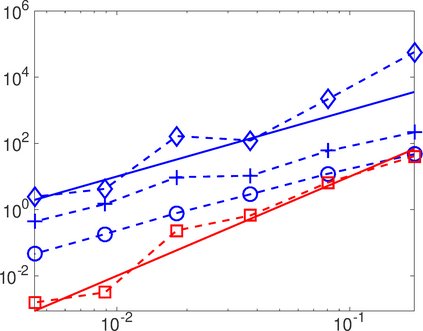
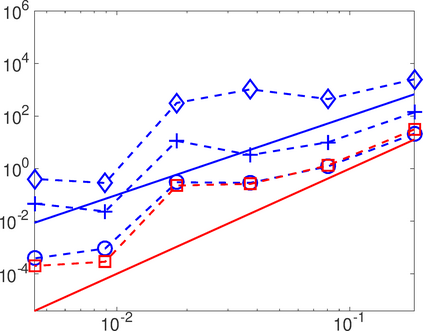
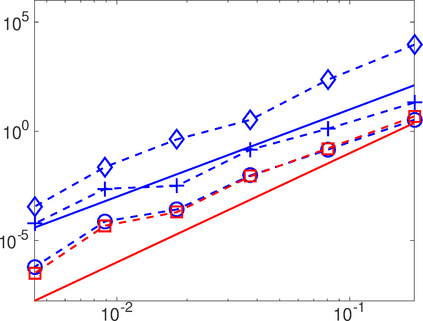
This work analyzes a high order hybridizable discontinuous Galerkin (HDG) method for the linear elasticity problem in a domain not necessarily polyhedral. The domain is approximated by a polyhedral computational domain where the HDG solution can be computed. The introduction of the rotation as one of the unknowns allows us to use the gradient of the displacements to obtain an explicit representation of the boundary data in the computational domain. The boundary data is transferred from the true boundary to the computational boundary by line integrals, where the integrand depends on the Cauchy stress tensor and the rotation. Under closeness assumptions between the computational and true boundaries, the scheme is shown to be well-posed and optimal error estimates are provided even in the nearly incompressible. Numerical experiments in two-dimensions are presented.