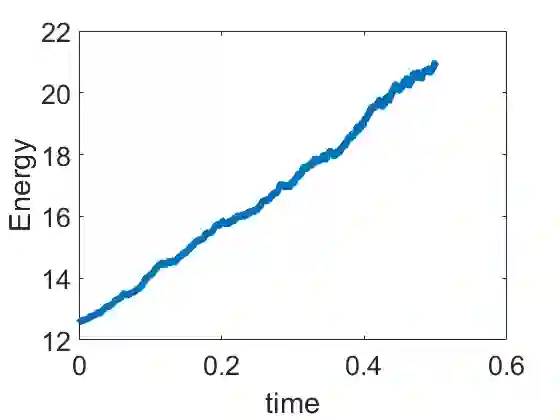
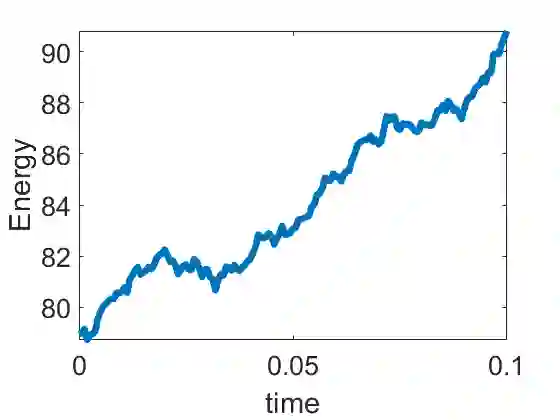
In this paper we propose and analyze finite element discontinuous Galerkin methods for the one- and two-dimensional stochastic Maxwell equations with multiplicative noise. The discrete energy law of the semi-discrete DG methods were studied. Optimal error estimate of the semi-discrete method is obtained for the one-dimensional case, and the two-dimensional case on both rectangular meshes and triangular meshes under certain mesh assumptions. Strong Taylor 2.0 scheme is used as the temporal discretization. Both one- and two-dimensional numerical results are presented to validate the theoretical analysis results.
翻译:在本文中,我们提出并分析了具有多倍噪音的一维和二维随机麦克斯韦尔方程式的有限元素不连续的Galerkin方法。研究了半分立的DG方法的离散能源法。对一维的半分解方法得出了最佳误差估计,对某些网状假设下矩形草和三角网舍的二维案例进行了最佳误差估计。强大的Taylor 2.0方案用作时间分解法。提出了一维和二维的数值结果,以验证理论分析结果。