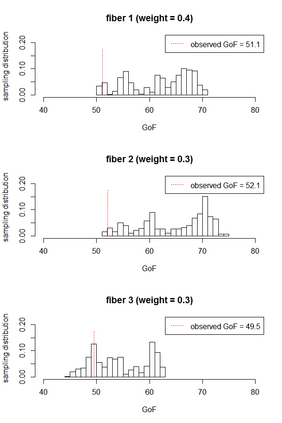
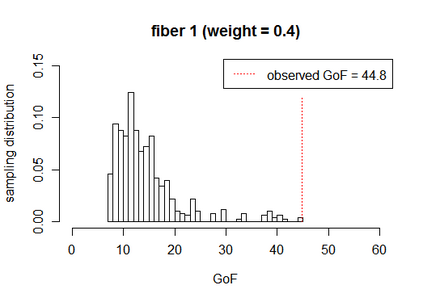
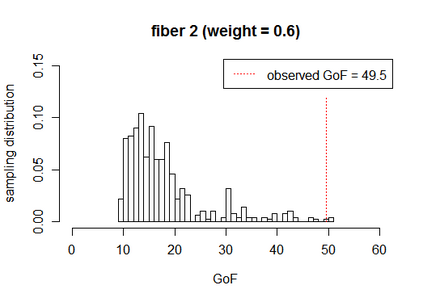
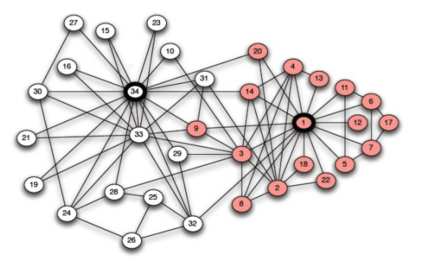
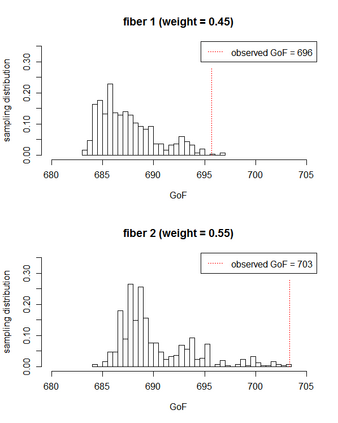
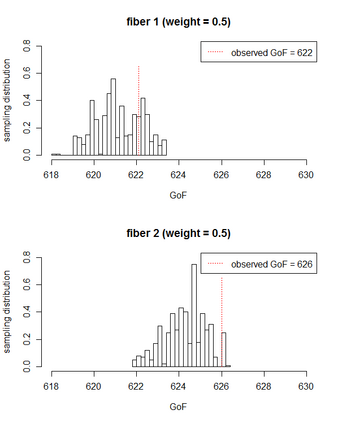
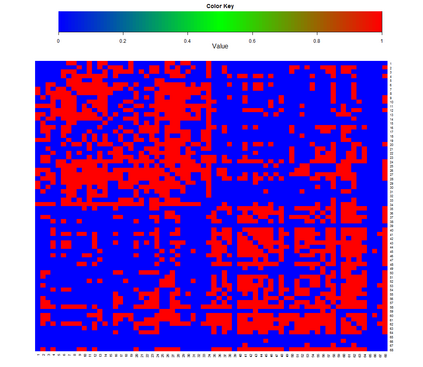
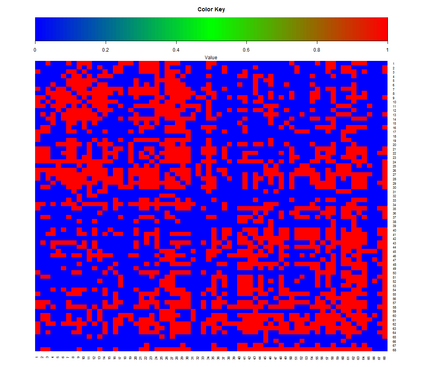
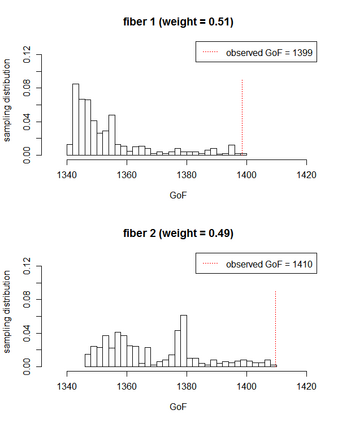
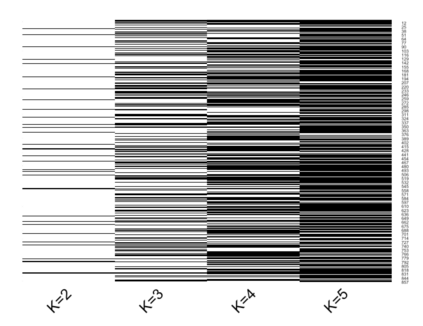
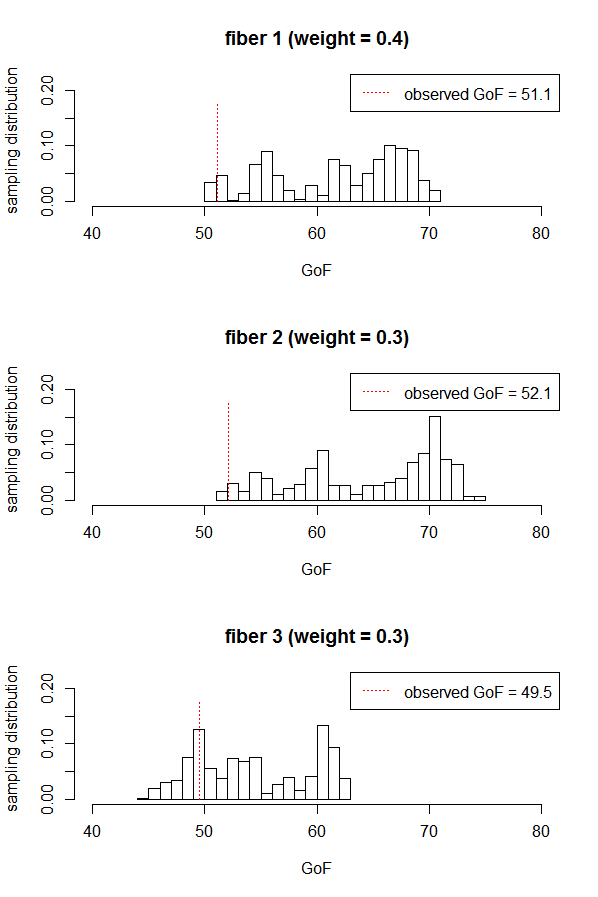
We construct Bayesian and frequentist finite-sample goodness-of-fit tests for three different variants of the stochastic blockmodel for network data. Since all of the stochastic blockmodel variants are log-linear in form when block assignments are known, the tests for the \emph{latent} block model versions combine a block membership estimator with the algebraic statistics machinery for testing goodness-of-fit in log-linear models. We describe Markov bases and marginal polytopes of the variants of the stochastic blockmodel, and discuss how both facilitate the development of goodness-of-fit tests and understanding of model behavior. The general testing methodology developed here extends to any finite mixture of log-linear models on discrete data, and as such is the first application of the algebraic statistics machinery for latent-variable models.
翻译:暂无翻译