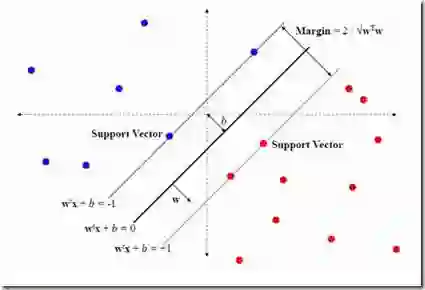
Support Vector Machines (SVM) have gathered significant acclaim as classifiers due to their successful implementation of Statistical Learning Theory. However, in the context of multiclass and multilabel settings, the reliance on vector-based formulations in existing SVM-based models poses limitations regarding flexibility and ease of incorporating additional terms to handle specific challenges. To overcome these limitations, our research paper focuses on introducing a matrix formulation for SVM that effectively addresses these constraints. By employing the Accelerated Gradient Descent method in the dual, we notably enhance the efficiency of solving the Matrix-SVM problem. Experimental evaluations on multilabel and multiclass datasets demonstrate that Matrix SVM achieves superior time efficacy while delivering similar results to Binary Relevance SVM. Moreover, our matrix formulation unveils crucial insights and advantages that may not be readily apparent in traditional vector-based notations. We emphasize that numerous multilabel models can be viewed as extensions of SVM, with customised modifications to meet specific requirements. The matrix formulation presented in this paper establishes a solid foundation for developing more sophisticated models capable of effectively addressing the distinctive challenges encountered in multilabel learning.
翻译:暂无翻译