Tensor-based Dinkelbach method for computing generalized tensor eigenvalues and its applications

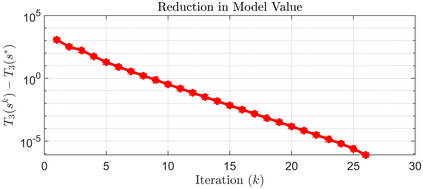
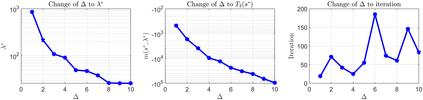
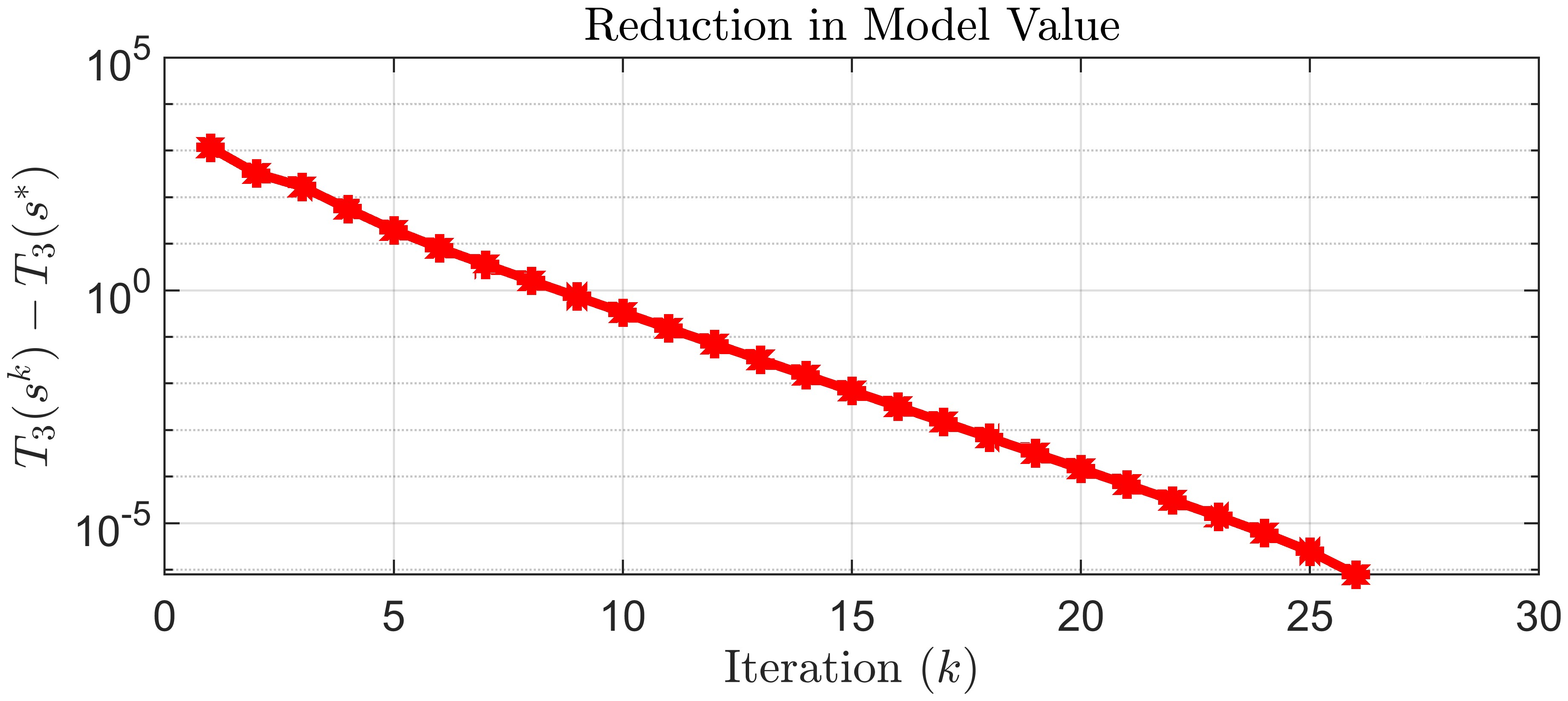
In this paper, we propose a novel tensor-based Dinkelbach--Type method for computing extremal tensor generalized eigenvalues. We show that the extremal tensor generalized eigenvalue can be reformulated as a critical subproblem of the classical Dinkelbach--Type method, which can subsequently be expressed as a multilinear optimization problem (MOP). The MOP is solved under a spherical constraint using an efficient proximal alternative minimization method, in which we rigorously establish the global convergence. Additionally, the equivalent MOP is reformulated as an unconstrained optimization problem, allowing for the analysis of the Kurdyka-Lojasiewicz (KL) exponent and providing an explicit expression for the convergence rate of the proposed algorithm. Preliminary numerical experiments on solving extremal tensor generalized eigenvalues and minimizing high-order trust-region subproblems are provided, validating the efficacy and practical utility of the proposed method.