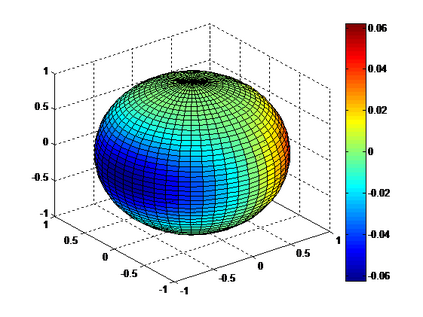
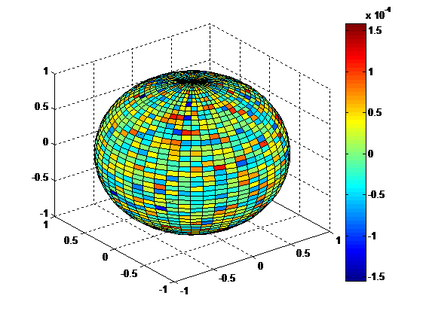
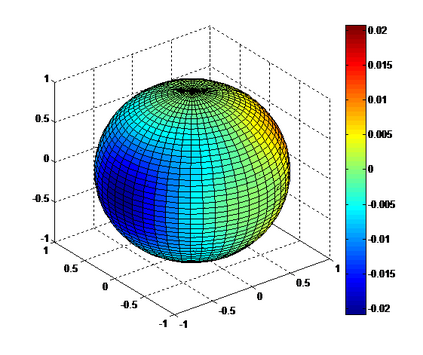
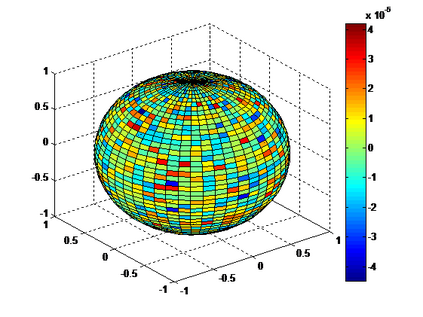
The Riesz transform of $u$ : $\mathcal{S}(\mathbb{R}^n) \rightarrow \mathcal{S'}(\mathbb{R}^n)$ is defined as a convolution by a singular kernel, and can be conveniently expressed using the Fourier Transform and a simple multiplier. We extend this analysis to higher order Riesz transforms, i.e. some type of singular integrals that contain tensorial polyadic kernels and define an integral transform for functions $\mathcal{S}(\mathbb{R}^n) \rightarrow \mathcal{S'}(\mathbb{R}^{ n \times n \times \dots n})$. We show that the transformed kernel is also a polyadic tensor, and propose a general method to compute explicitely the Fourier mutliplier. Analytical results are given, as well as a recursive algorithm, to compute the coefficients of the transformed kernel. We compare the result to direct numerical evaluation, and discuss the case $n=2$, with application to image analysis.
翻译:Riesz 变换 $ 美元 : $\ mathcal{S} (\ mathbb{R ⁇ n)\ right carrow \ mathcal{S} (\ mathbb{R ⁇ n) 定义为单内核的熔化, 可以用 Fourier 变形和一个简单的乘数来方便表达。 我们把这个分析扩展至 更高级的 Riesz 变换, 即 含有 Exoral 多元内核并定义函数整体变换 $\ mathcal{S} (\\ mathbbb{R ⁇ n)\ rightrow\ mathcal{S} (\\ mathcal{S}\\\\\\ mathbb{r\\ n\ time n\time n\time\ dots n} $ 。 我们显示, 变换内核也是 多元 10, 并且 提议一种直译 4er 调 调 4 调调调色调色调色的普通方法。 。 分析结果, 以及一种循环算法, 和 将结果与 美元 直判判判判 = 数字分析。