DQMIX: A Distributional Perspective on Multi-Agent Reinforcement Learning

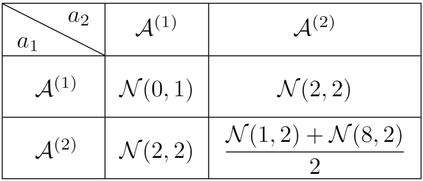
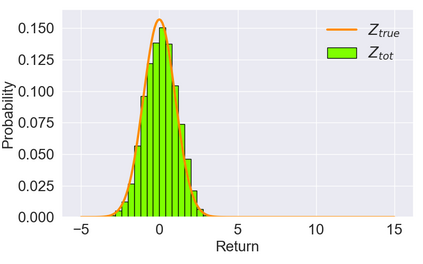
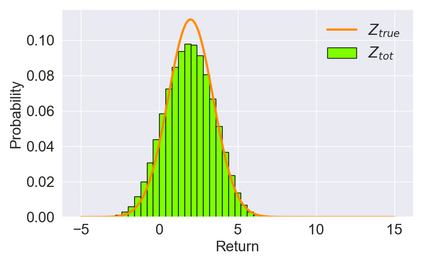
In cooperative multi-agent tasks, a team of agents jointly interact with an environment by taking actions, receiving a team reward and observing the next state. During the interactions, the uncertainty of environment and reward will inevitably induce stochasticity in the long-term returns and the randomness can be exacerbated with the increasing number of agents. However, most of the existing value-based multi-agent reinforcement learning (MARL) methods only model the expectations of individual Q-values and global Q-value, ignoring such randomness. Compared to the expectations of the long-term returns, it is more preferable to directly model the stochasticity by estimating the returns through distributions. With this motivation, this work proposes DQMIX, a novel value-based MARL method, from a distributional perspective. Specifically, we model each individual Q-value with a categorical distribution. To integrate these individual Q-value distributions into the global Q-value distribution, we design a distribution mixing network, based on five basic operations on the distribution. We further prove that DQMIX satisfies the \emph{Distributional-Individual-Global-Max} (DIGM) principle with respect to the expectation of distribution, which guarantees the consistency between joint and individual greedy action selections in the global Q-value and individual Q-values. To validate DQMIX, we demonstrate its ability to factorize a matrix game with stochastic rewards. Furthermore, the experimental results on a challenging set of StarCraft II micromanagement tasks show that DQMIX consistently outperforms the value-based multi-agent reinforcement learning baselines.