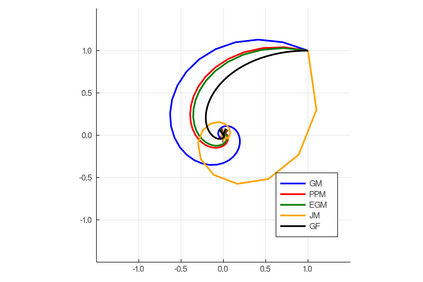
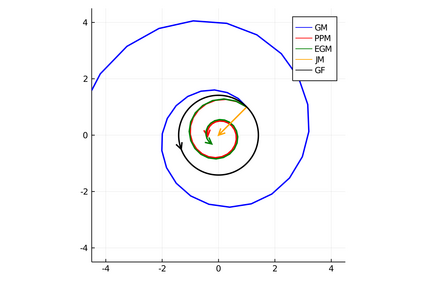
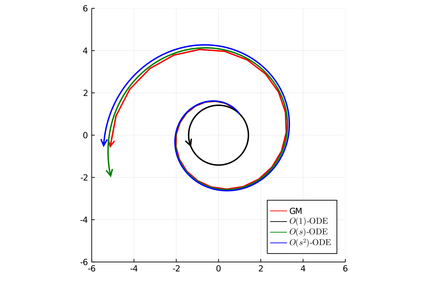
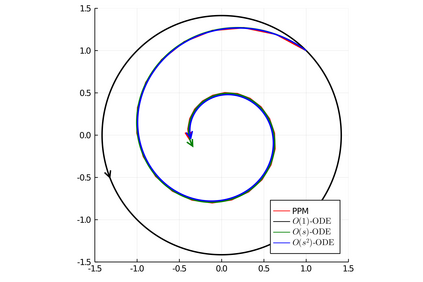
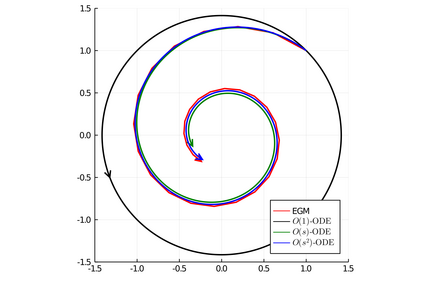
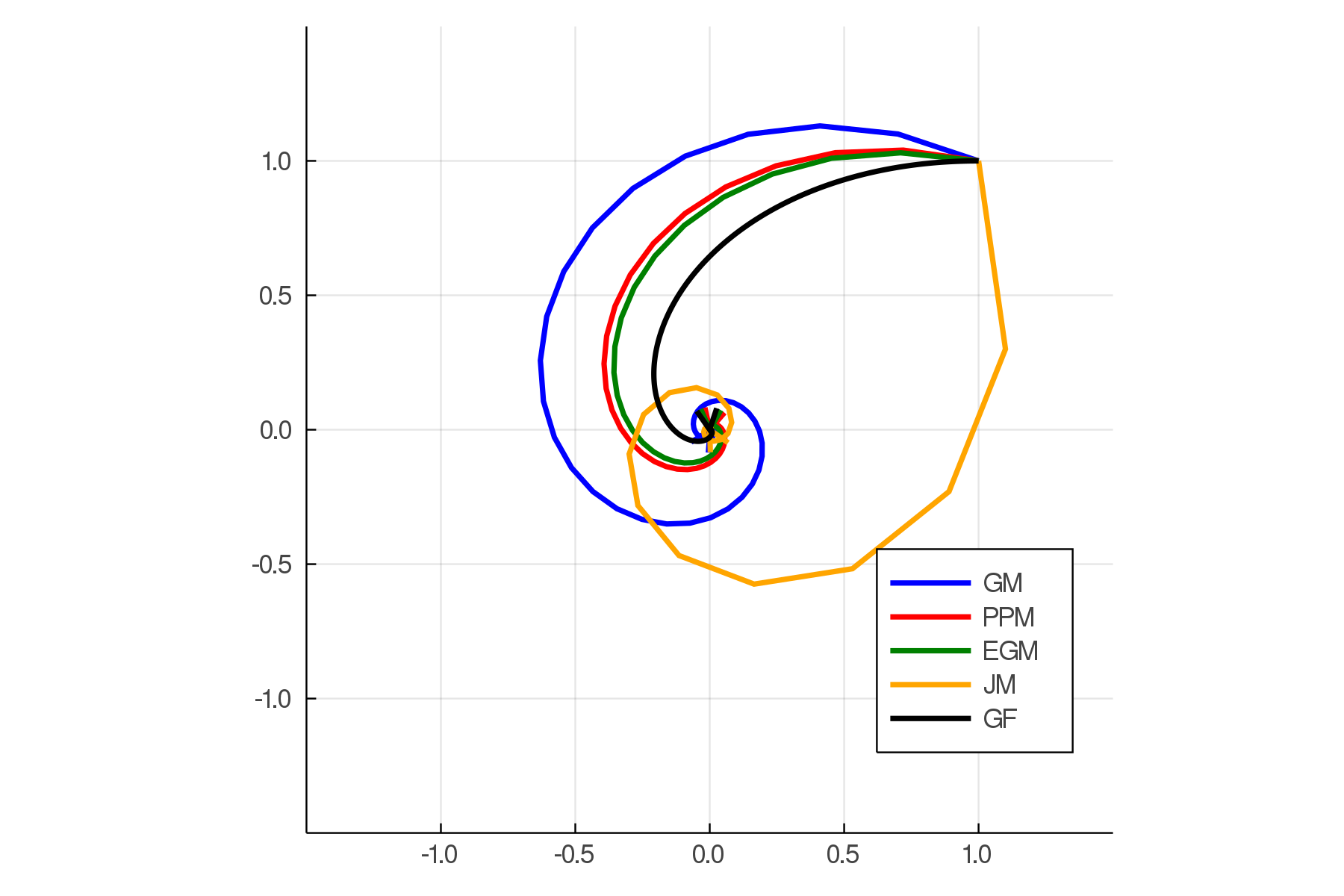
There has been a long history of using ordinary differential equations (ODEs) to understand the dynamics of discrete-time algorithms (DTAs). Surprisingly, there are still two fundamental and unanswered questions: (i) it is unclear how to obtain a \emph{suitable} ODE from a given DTA, and (ii) it is unclear the connection between the convergence of a DTA and its corresponding ODEs. In this paper, we propose a new machinery -- an $O(s^r)$-resolution ODE framework -- for analyzing the behavior of a generic DTA, which (partially) answers the above two questions. The framework contains three steps: 1. To obtain a suitable ODE from a given DTA, we define a hierarchy of $O(s^r)$-resolution ODEs of a DTA parameterized by the degree $r$, where $s$ is the step-size of the DTA. We present a principal approach to construct the unique $O(s^r)$-resolution ODEs from a DTA; 2. To analyze the resulting ODE, we propose the $O(s^r)$-linear-convergence condition of a DTA with respect to an energy function, under which the $O(s^r)$-resolution ODE converges linearly to an optimal solution; 3. To bridge the convergence properties of a DTA and its corresponding ODEs, we define the properness of an energy function and show that the linear convergence of the $O(s^r)$-resolution ODE with respect to a proper energy function can automatically guarantee the linear convergence of the DTA. To better illustrate this machinery, we utilize it to study three classic algorithms -- gradient descent ascent (GDA), proximal point method (PPM) and extra-gradient method (EGM) -- for solving the unconstrained minimax problem $\min_{x\in\RR^n} \max_{y\in \RR^m} L(x,y)$.
翻译:使用普通差异方程式( ODEs) 来理解离散时间算法( DTAs) 的动态。 令人惊讶的是, 仍然有两个根本性和未解的问题:( 一) 如何从给定的 DTA 获得一个 emph{ 直观的 ODE, 以及 (二) 使用 DTA 的趋同和相应的 ODE 之间的关联是模糊的。 在本文中, 我们提出一个新的机制 -- -- 一个 $( r) 解析的 ODE 框架 -- -- 用于分析通用 DTA 的行为, (部分) 解答上述两个问题。 框架包含三个步骤 : 1. 要从给定的 DTATA 获得一个合适的 Odemode, 我们定义了以 $( s) 美元为参数的 DTA( modeal- moreal) 解算的 。 我们提出一种主要方法, 用来从 DTATA 中构建一个独特的 $( r) 解算的 解算的 Rental- dealal dealal demode Or 。