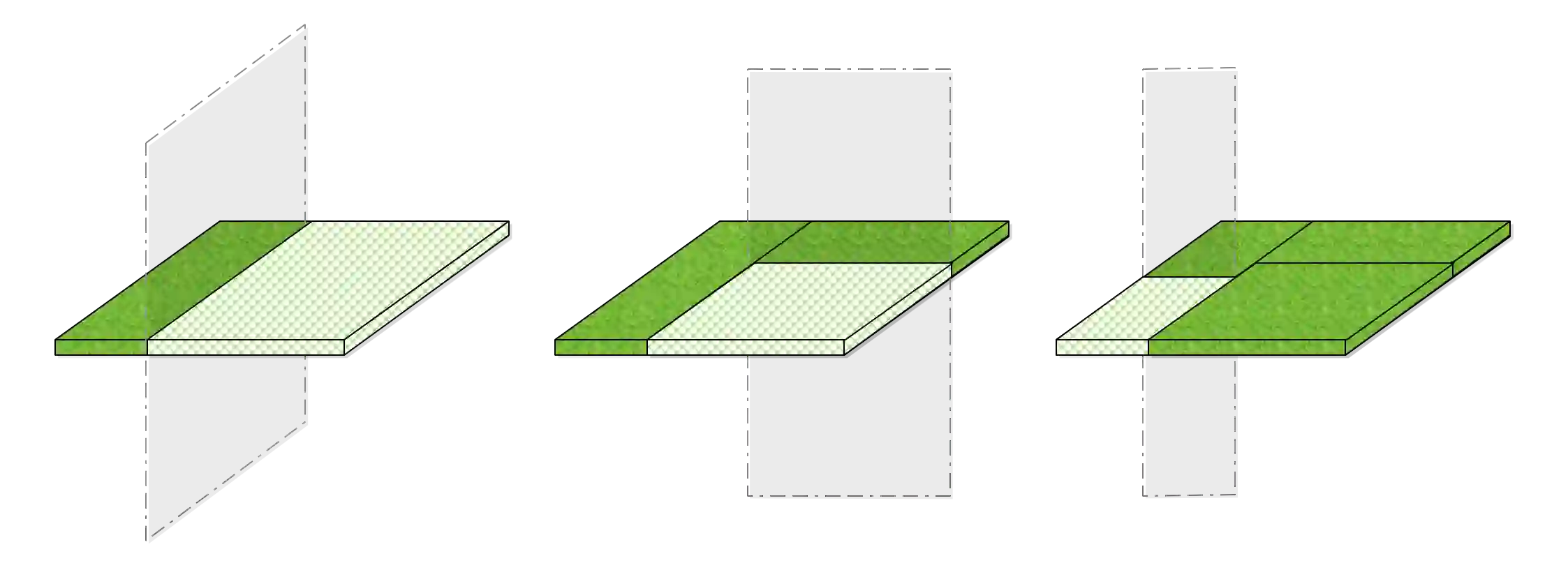
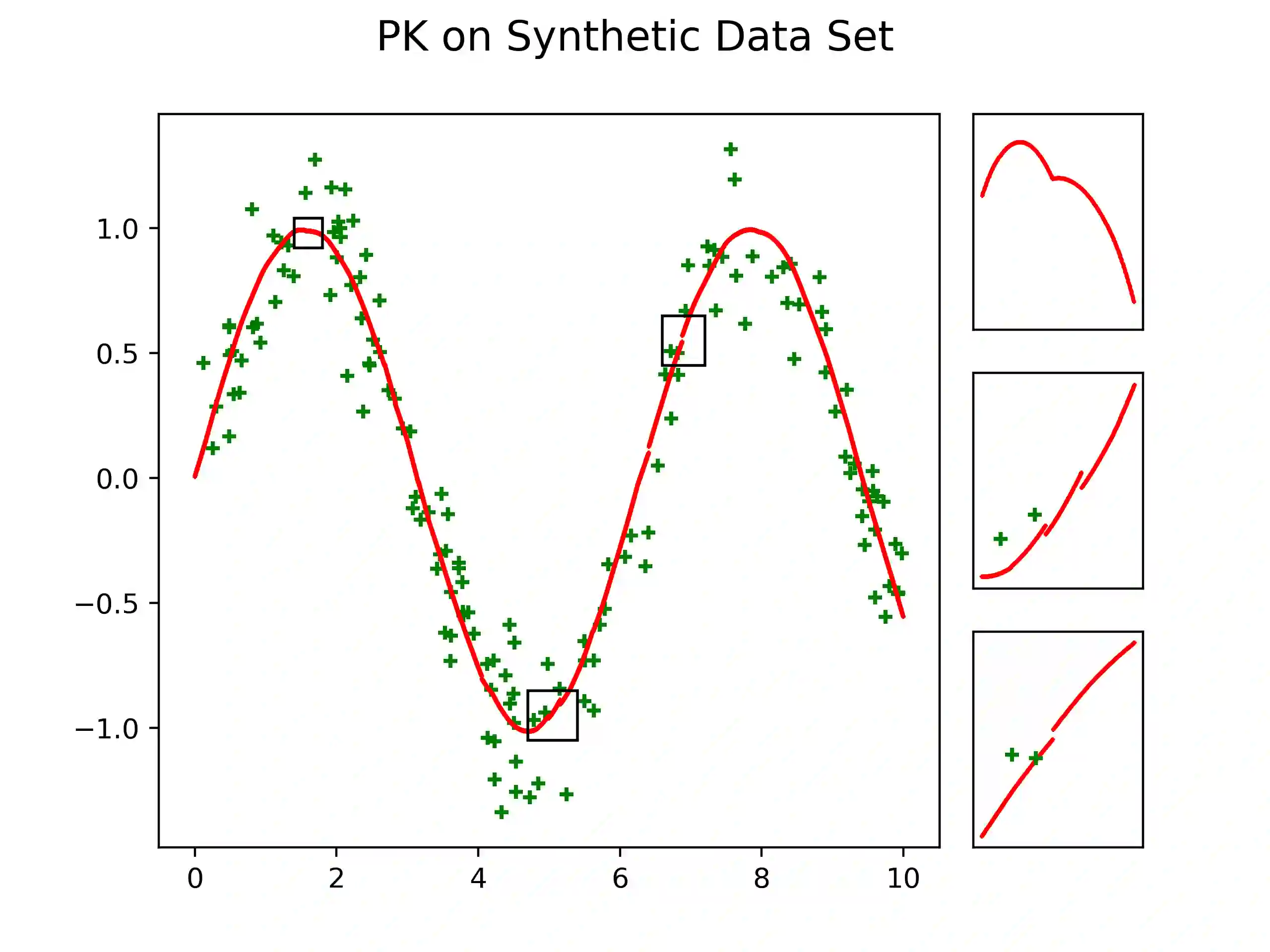
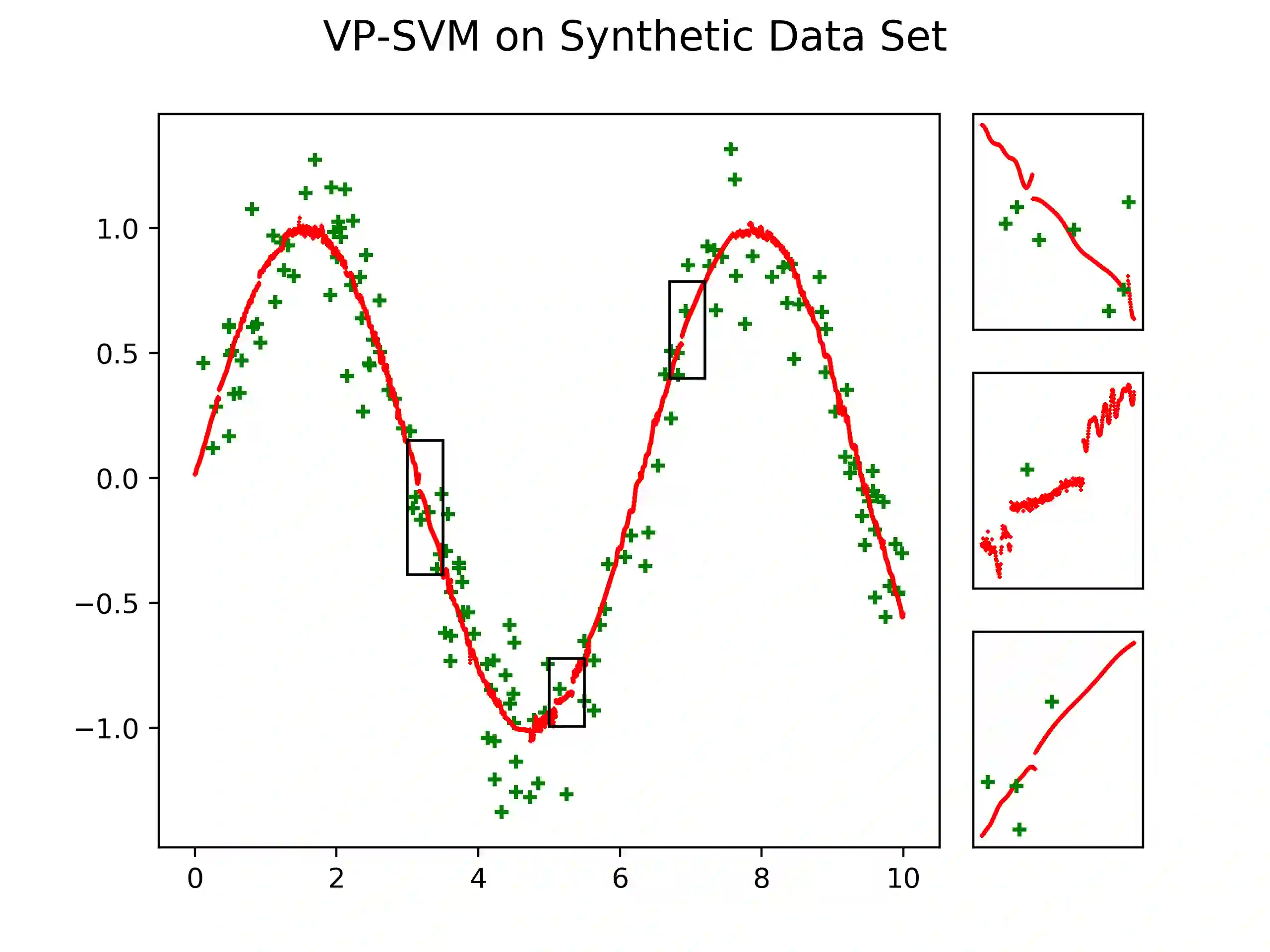
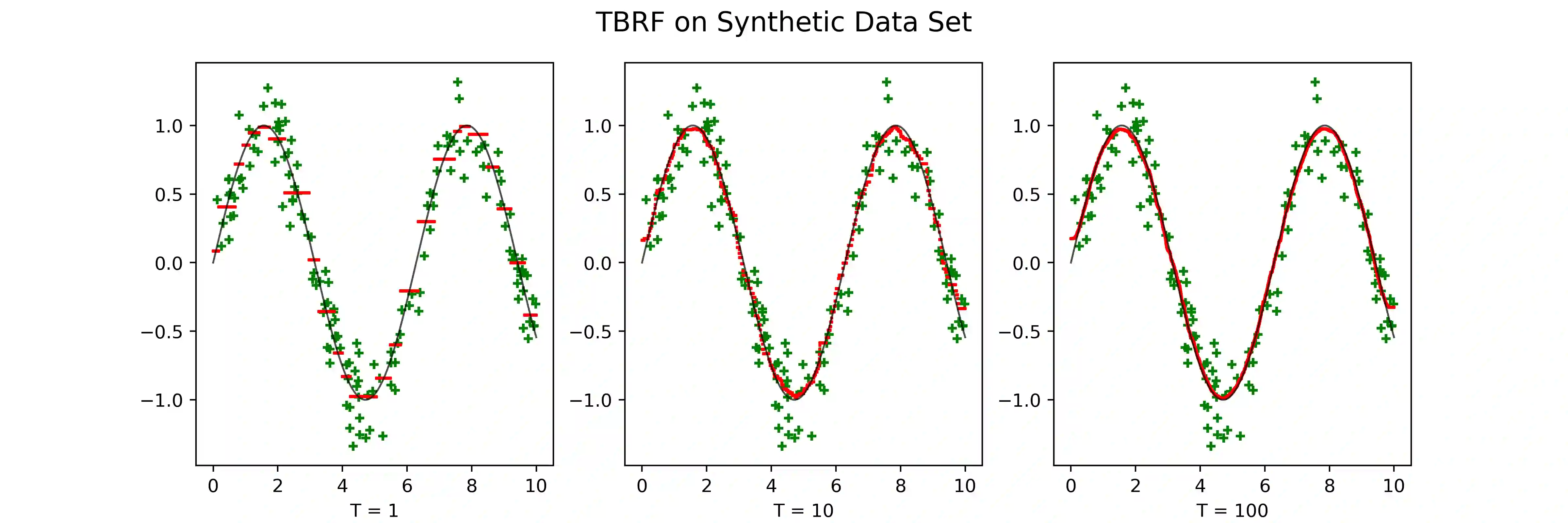
We propose a novel method designed for large-scale regression problems, namely the two-stage best-scored random forest (TBRF). "Best-scored" means to select one regression tree with the best empirical performance out of a certain number of purely random regression tree candidates, and "two-stage" means to divide the original random tree splitting procedure into two: In stage one, the feature space is partitioned into non-overlapping cells; in stage two, child trees grow separately on these cells. The strengths of this algorithm can be summarized as follows: First of all, the pure randomness in TBRF leads to the almost optimal learning rates, and also makes ensemble learning possible, which resolves the boundary discontinuities long plaguing the existing algorithms. Secondly, the two-stage procedure paves the way for parallel computing, leading to computational efficiency. Last but not least, TBRF can serve as an inclusive framework where different mainstream regression strategies such as linear predictor and least squares support vector machines (LS-SVMs) can also be incorporated as value assignment approaches on leaves of the child trees, depending on the characteristics of the underlying data sets. Numerical assessments on comparisons with other state-of-the-art methods on several large-scale real data sets validate the promising prediction accuracy and high computational efficiency of our algorithm.
翻译:我们提出一个针对大规模回归问题的新颖方法,即两阶段最精细随机森林(TBRF)。“最精细”是指从某些纯粹随机回归树候选者中选择一棵回归树,其最佳实证性表现最佳,而“两阶段”是指将原始随机树分成两个程序:在第一阶段,特征空间被分割成不重叠的细胞;在第二阶段,儿童树在这些细胞上分别生长。这一算法的优点可以概括如下:首先,TBRF的纯随机性导致几乎最佳的学习率,并使得共同学习成为可能,这解决了长期阻碍现有算法的边界不连续性。第二,两阶段程序为平行计算铺平了道路,导致计算效率。最后但并非最不重要的一点是,TBRF可以作为一个包容性框架,在这个框架内,不同的主流回归战略,如线性预测器和最小平方支持矢量机(LS-SVMS)也可以作为儿童树树叶上的价值分配方法,这要取决于我们高估测算法的高级数据集的特性。