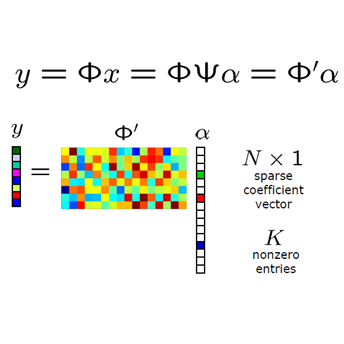
As a signal recovery algorithm, compressed sensing is particularly useful when the data has low-complexity and samples are rare, which matches perfectly with the task of quantum phase estimation (QPE). In this work we present a new Heisenberg-limited QPE algorithm for early quantum computers based on compressed sensing. More specifically, given many copies of a proper initial state and queries to some unitary operators, our algorithm is able to recover the frequency with a total runtime $\mathcal{O}(\epsilon^{-1}\text{poly}\log(\epsilon^{-1}))$, where $\epsilon$ is the accuracy. Moreover, the maximal runtime satisfies $T_{\max}\epsilon \ll \pi$, which is comparable to the state of art algorithms, and our algorithm is also robust against certain amount of noise from sampling. We also consider the more general quantum eigenvalue estimation problem (QEEP) and show numerically that the off-grid compressed sensing can be a strong candidate for solving the QEEP.
翻译:暂无翻译