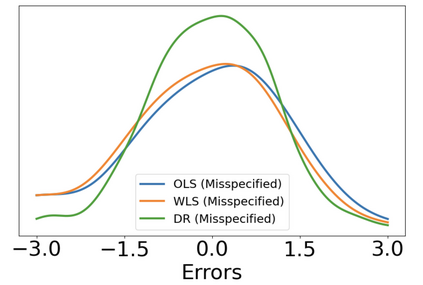
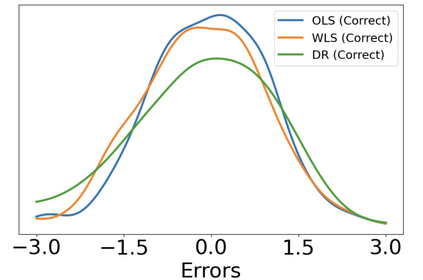
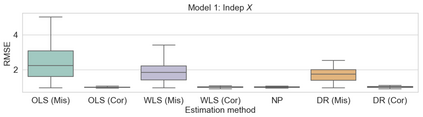
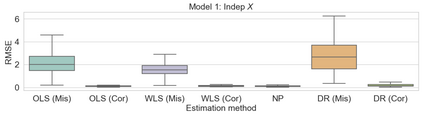
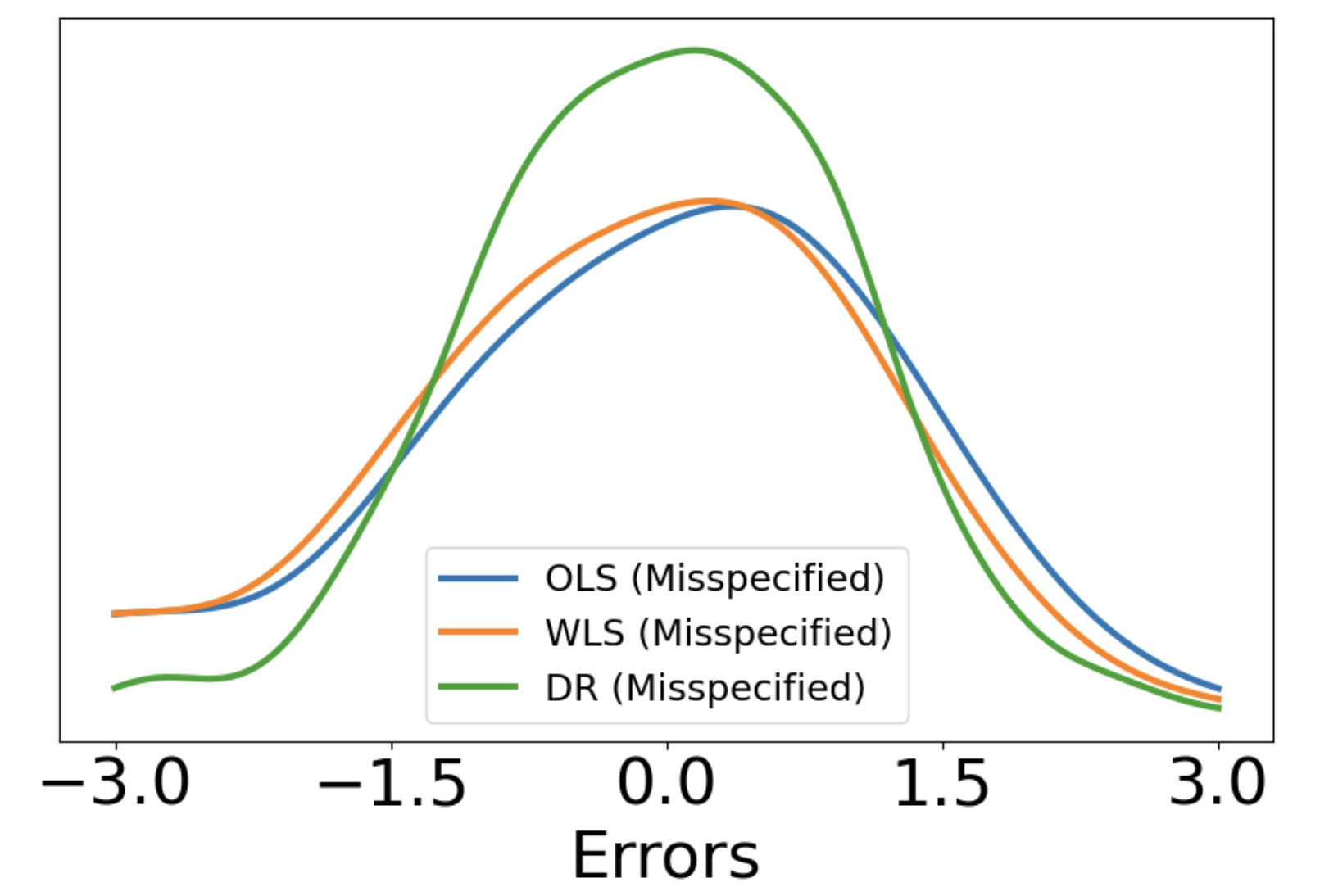
Consider a scenario where we have access to train data with both covariates and outcomes while test data only contains covariates. In this scenario, our primary aim is to predict the missing outcomes of the test data. With this objective in mind, we train parametric regression models under a covariate shift, where covariate distributions are different between the train and test data. For this problem, existing studies have proposed covariate shift adaptation via importance weighting using the density ratio. This approach averages the train data losses, each weighted by an estimated ratio of the covariate densities between the train and test data, to approximate the test-data risk. Although it allows us to obtain a test-data risk minimizer, its performance heavily relies on the accuracy of the density ratio estimation. Moreover, even if the density ratio can be consistently estimated, the estimation errors of the density ratio also yield bias in the estimators of the regression model's parameters of interest. To mitigate these challenges, we introduce a doubly robust estimator for covariate shift adaptation via importance weighting, which incorporates an additional estimator for the regression function. Leveraging double machine learning techniques, our estimator reduces the bias arising from the density ratio estimation errors. We demonstrate the asymptotic distribution of the regression parameter estimator. Notably, our estimator remains consistent if either the density ratio estimator or the regression function is consistent, showcasing its robustness against potential errors in density ratio estimation. Finally, we confirm the soundness of our proposed method via simulation studies.
翻译:暂无翻译