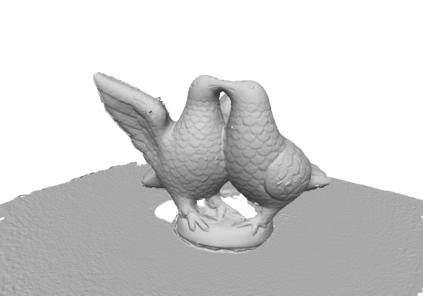
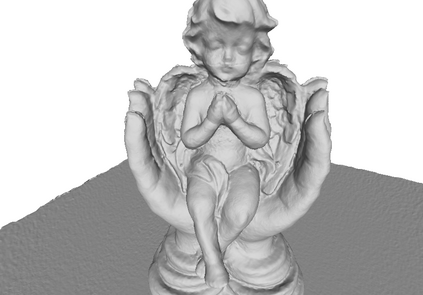
Mesh refinement is a fundamental step for accurate Multi-View Stereo. It modifies the geometry of an initial manifold mesh to minimize the photometric error induced in a set of camera pairs. This initial mesh is usually the output of volumetric 3D reconstruction based on min-cut over Delaunay Triangulations. Such methods produce a significant amount of non-manifold vertices, therefore they require a vertex split step to explicitly repair them. In this paper, we extend this method to preemptively fix the non-manifold vertices by reasoning directly on the Delaunay Triangulation and avoid most vertex splits. The main contribution of this paper addresses the problem of choosing the camera pairs adopted by the refinement process. We treat the problem as a mesh labeling process, where each label corresponds to a camera pair. Differently from the state-of-the-art methods, which use each camera pair to refine all the visible parts of the mesh, we choose, for each facet, the best pair that enforces both the overall visibility and coverage. The refinement step is applied for each facet using only the camera pair selected. This facetwise refinement helps the process to be applied in the most evenly way possible.
翻译:网状精细是准确多视图立体的根本性步骤。 它会修改初始多元网格的几何, 以最小化一组相配相机中引出的光度误差 。 这个初始网格通常是基于 Delaunay 三角配对的小切的体积 3D 重建的输出。 这种方法产生大量非自制的脊椎, 因此它们需要一个顶部分裂的步骤来明确修复它们 。 在本文中, 我们通过直接在 Delaunay 三角形上进行推理, 来先发制人地修正非自定义的脊椎 。 此纸的主要贡献解决了选择在精细化过程中采用的相配相机的问题 。 我们将此问题当作一个网格标签过程处理, 每个标签与相配相匹配。 不同的是, 使用每张相配相机来精细化所有可见的部位, 我们选择每张脸部最好的一对, 使用最精细的步骤来改进每张的镜头。 最精确的一步只能用最精确的方法来改进每张脸。