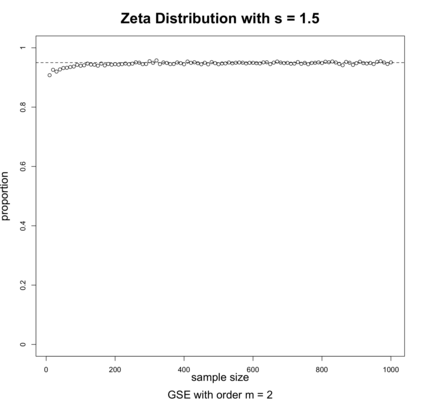
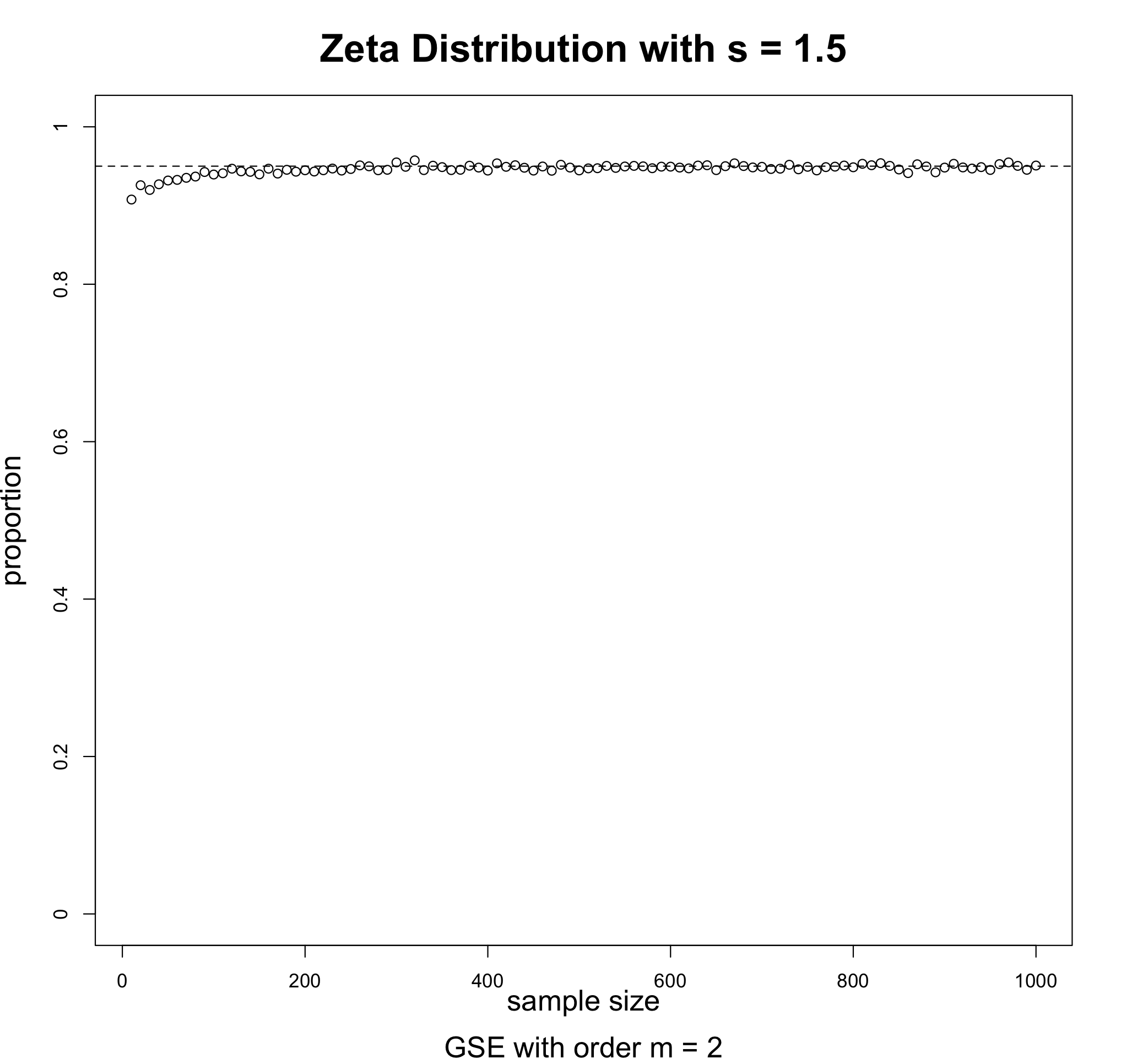
Shannon's entropy is one of the building blocks of information theory and an essential aspect of Machine Learning methods (e.g., Random Forests). Yet, it is only finitely defined for distributions with fast decaying tails on a countable alphabet. The unboundedness of Shannon's entropy over the general class of all distributions on an alphabet prevents its potential utility from being fully realized. To fill the void in the foundation of information theory, Zhang (2020) proposed generalized Shannon's entropy, which is finitely defined everywhere. The plug-in estimator, adopted in almost all entropy-based ML method packages, is one of the most popular approaches to estimating Shannon's entropy. The asymptotic distribution for Shannon's entropy's plug-in estimator was well studied in the existing literature. This paper studies the asymptotic properties for the plug-in estimator of generalized Shannon's entropy on countable alphabets. The developed asymptotic properties require no assumptions on the original distribution. The proposed asymptotic properties allow interval estimation and statistical tests with generalized Shannon's entropy.
翻译:香农的昆虫是信息理论的基石之一,也是机器学习方法(如随机森林)的一个基本方面。然而,它仅有限地被定义为在可计算字母上以快速腐烂尾巴进行分布。香农的昆虫在以字母进行所有分布的普通类上的无约束性使其潜在效用无法完全实现。为填补信息理论基础的空白,张(202020)提议对香农的昆虫普遍化,到处都有有限的定义。几乎在所有基于酶的ML方法包中都采用了插座测量仪,这是估算香农的酶的最受欢迎的方法之一。香农的酶插座的无约束性分布在现有的文献中得到了很好的研究。本文件研究了普遍香农的插座估计仪的吸附性属性,在可计算字母上都有有限的定义。在几乎所有基于酶基的宏图法的包中,开发的充份属性不需要在原始分布上作任何假设。拟议的香农的香农的生长特性允许对原分布进行普遍化的统计性估测。