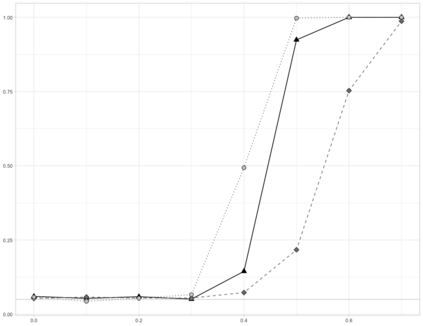
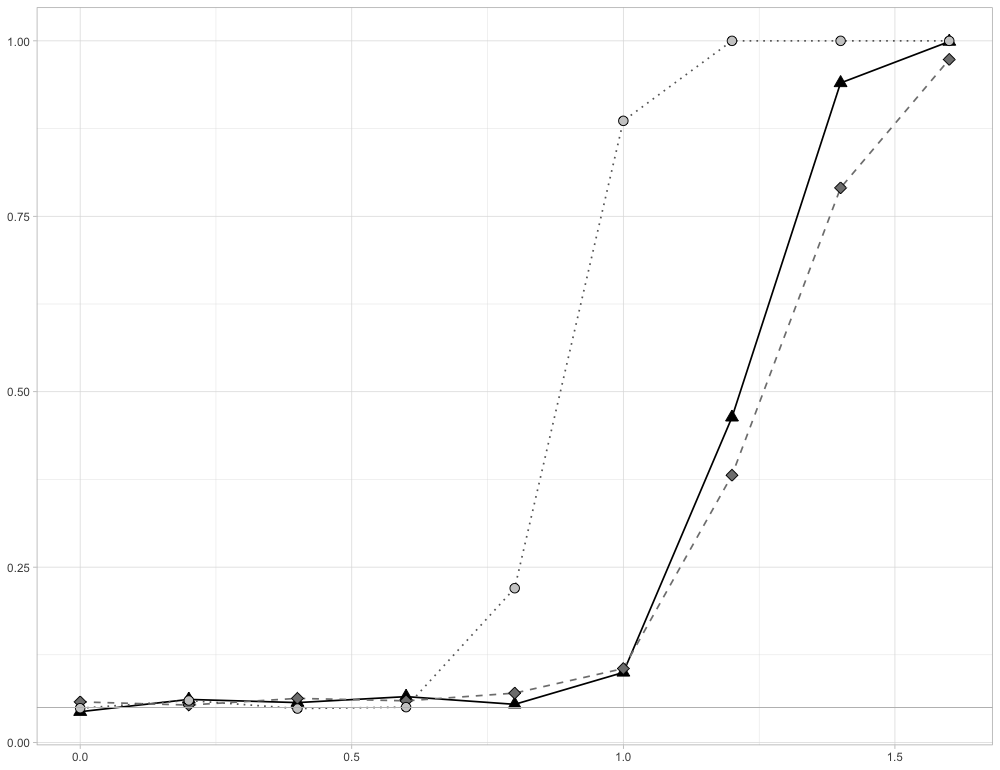
Independent $p$-dimensional vectors with independent complex or real valued entries such that $\mathbb{E} [\mathbf{x}_i] = \mathbf{0}$, ${\rm Var } (\mathbf{x}_i) = \mathbf{I}_p$, $i=1, \ldots,n$, let $\mathbf{T }_n$ be a $p \times p$ Hermitian nonnegative definite matrix and $f $ be a given function. We prove that an approriately standardized version of the stochastic process $ \big ( {\operatorname{tr}} ( f(\mathbf{B}_{n,t}) ) \big )_{t \in [t_0, 1]} $ corresponding to a linear spectral statistic of the sequential empirical covariance estimator $$ \big ( \mathbf{B}_{n,t} )_{t\in [ t_0 , 1]} = \Big ( \frac{1}{n} \sum_{i=1}^{\lfloor n t \rfloor} \mathbf{T }^{1/2}_n \mathbf{x}_i \mathbf{x}_i ^\star \mathbf{T }^{1/2}_n \Big)_{t\in [ t_0 , 1]} $$ converges weakly to a non-standard Gaussian process for $n,p\to\infty$. As an application we use these results to develop a novel approach for monitoring the sphericity assumption in a high-dimensional framework, even if the dimension of the underlying data is larger than the sample size.
翻译:独立的 $p$ 维矢量, 具有独立复杂或真实价值的条目 $mathbb{T}, [\ mathbf{x ⁇ i] =\ mathbf{0} 美元, $rm Var} (\ mathbf{x ⁇ i) = mathbf{I=1, \ldot} 美元, $\ mathb{T} 美元是 美元 =时间 p$ Hermitian 非阴性矩阵 和 $f 美元是给定的函数 。 我们证明, 相当标准的 进程 $\ rb{x} 标准值 {tr\\\\\\ ma\\\ xx} 数据( f\ b_, t_ f_0} t\\ f_ f_ 底值 的值值) 和这些测试结果的直线光度统计 [xxxxxxx=xxxxxxxxxx