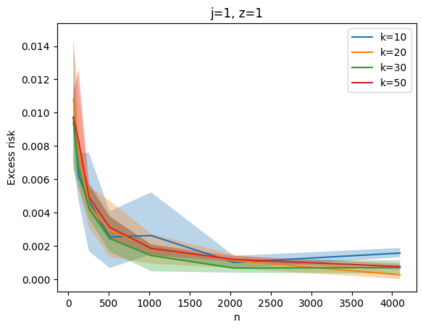
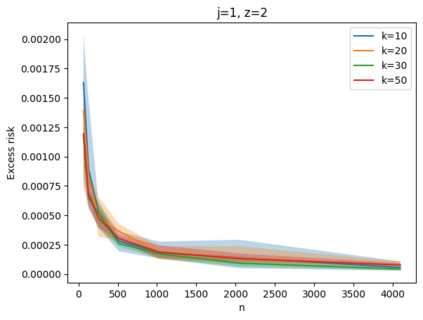
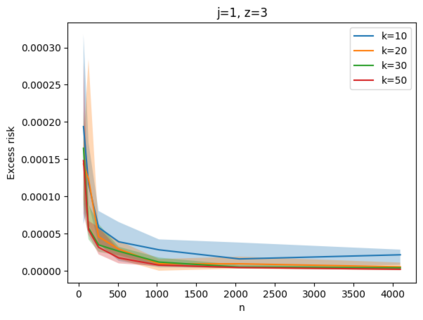
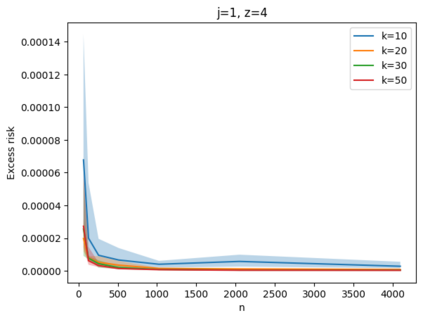
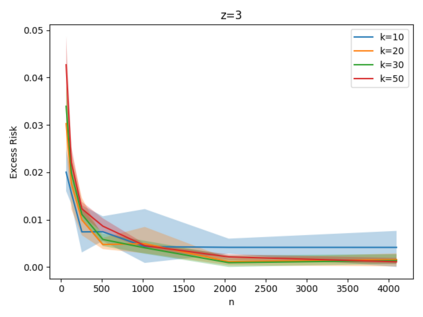
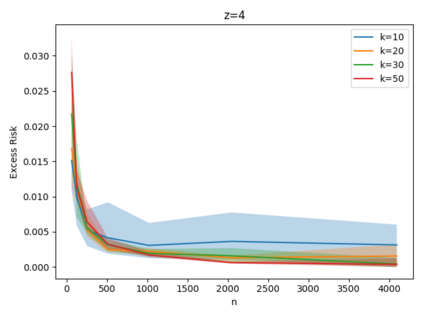
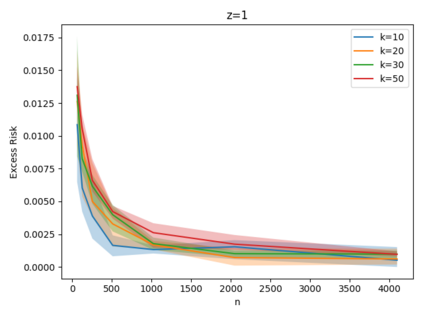
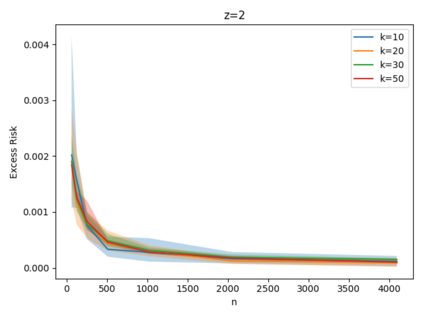
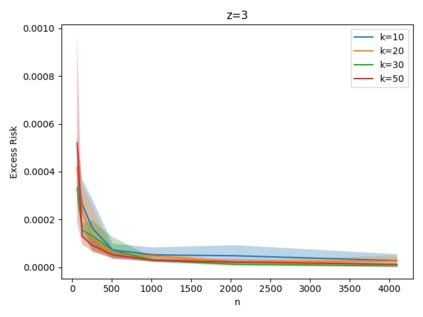
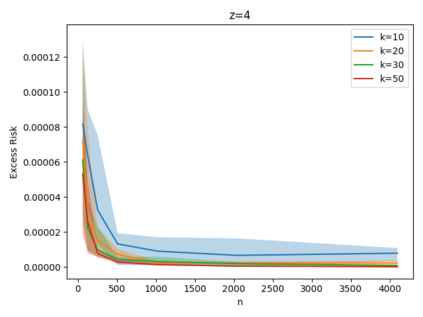
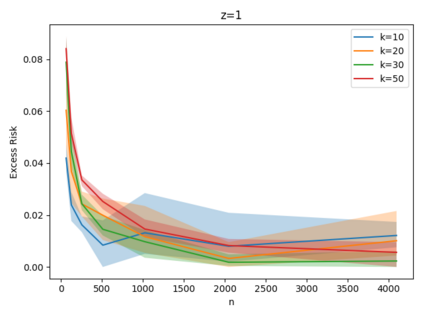
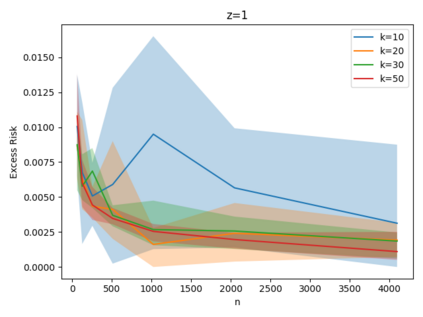
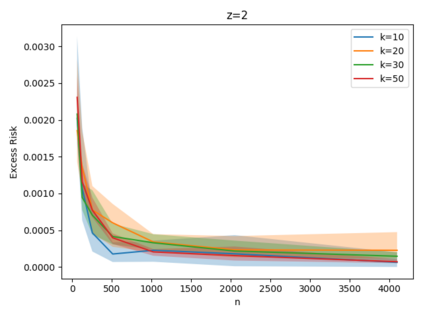
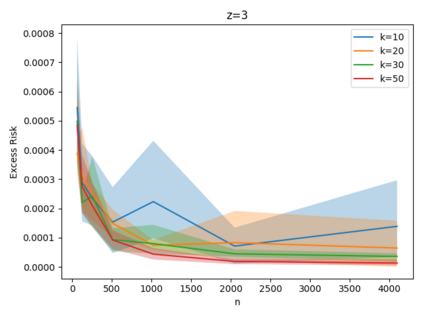
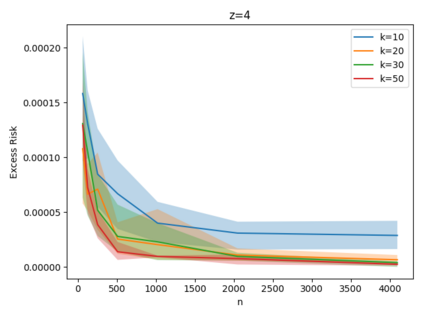
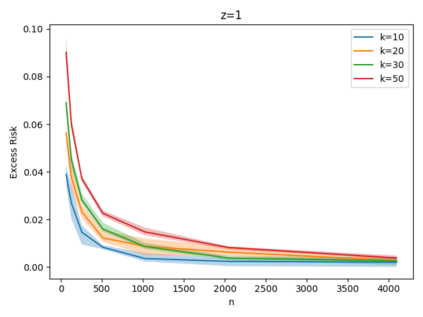
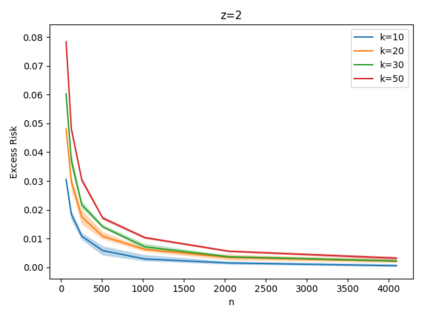
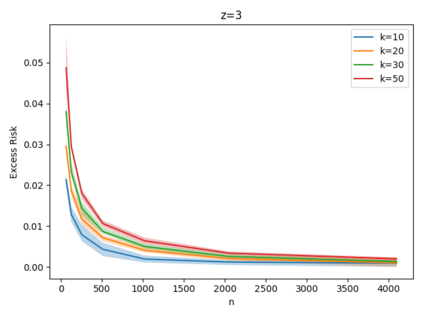
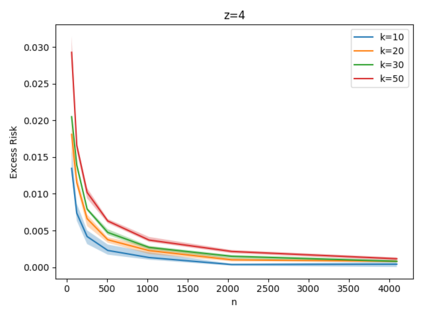
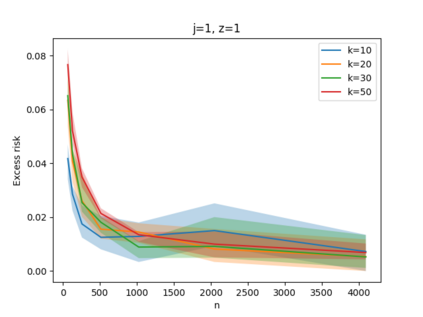
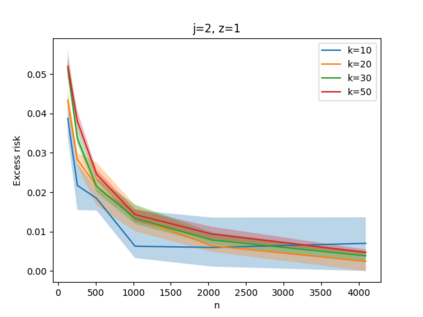
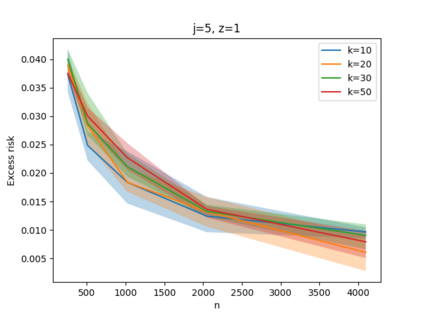
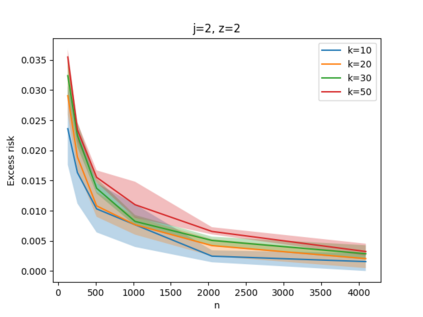
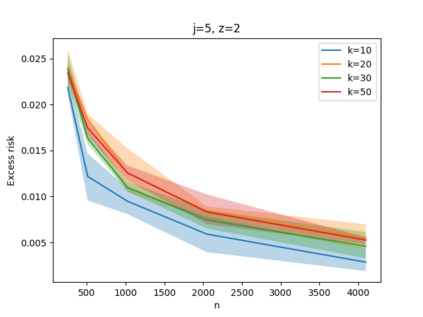
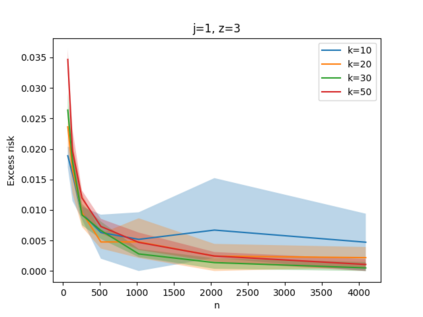
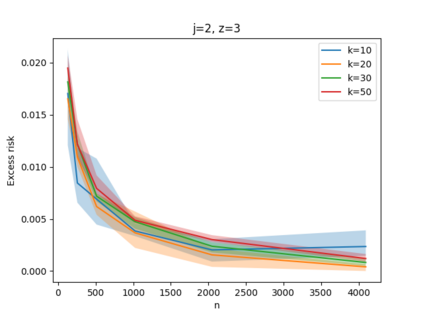
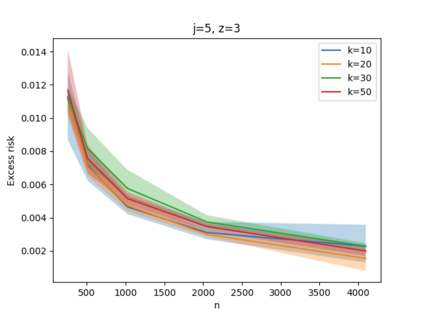
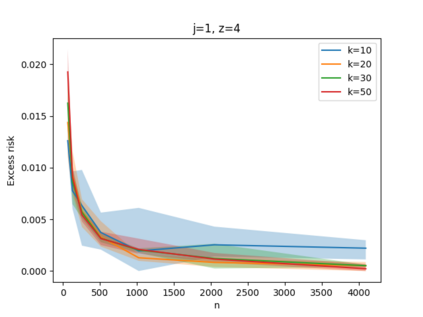
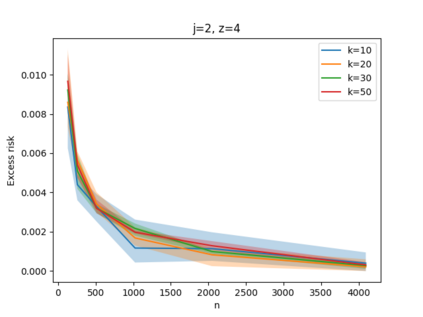
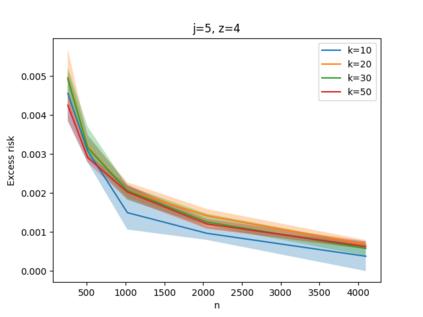
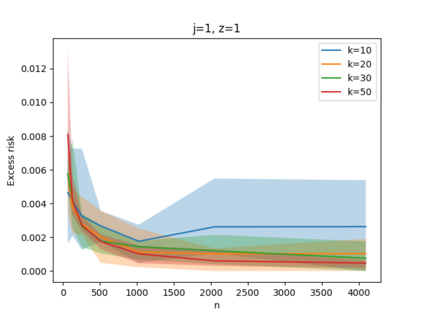
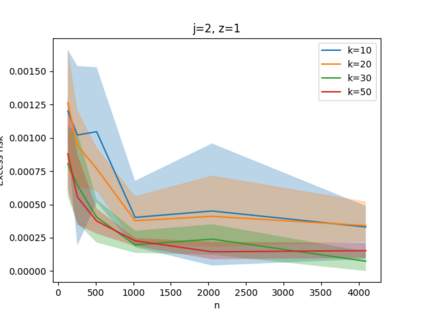
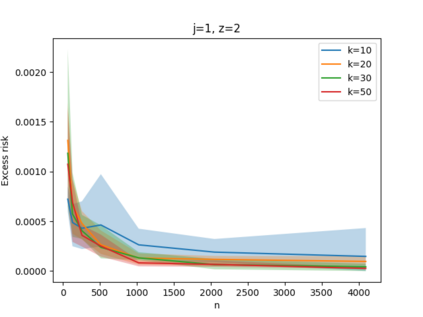
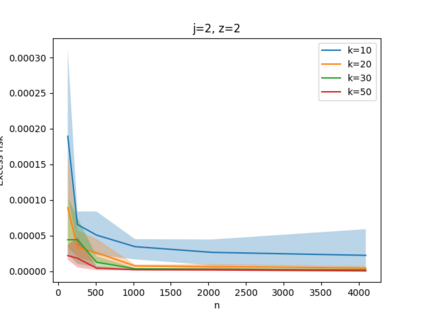
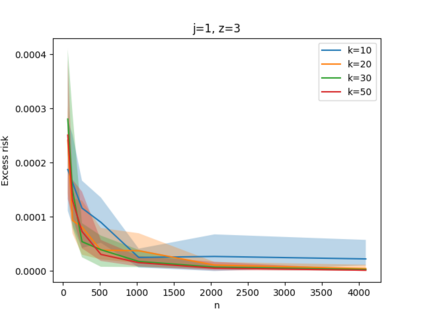
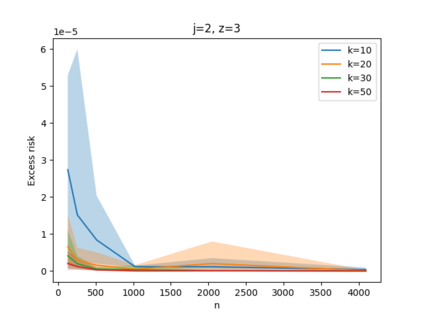
Given a set of points, clustering consists of finding a partition of a point set into $k$ clusters such that the center to which a point is assigned is as close as possible. Most commonly, centers are points themselves, which leads to the famous $k$-median and $k$-means objectives. One may also choose centers to be $j$ dimensional subspaces, which gives rise to subspace clustering. In this paper, we consider learning bounds for these problems. That is, given a set of $n$ samples $P$ drawn independently from some unknown, but fixed distribution $\mathcal{D}$, how quickly does a solution computed on $P$ converge to the optimal clustering of $\mathcal{D}$? We give several near optimal results. In particular, For center-based objectives, we show a convergence rate of $\tilde{O}\left(\sqrt{{k}/{n}}\right)$. This matches the known optimal bounds of [Fefferman, Mitter, and Narayanan, Journal of the Mathematical Society 2016] and [Bartlett, Linder, and Lugosi, IEEE Trans. Inf. Theory 1998] for $k$-means and extends it to other important objectives such as $k$-median. For subspace clustering with $j$-dimensional subspaces, we show a convergence rate of $\tilde{O}\left(\sqrt{\frac{kj^2}{n}}\right)$. These are the first provable bounds for most of these problems. For the specific case of projective clustering, which generalizes $k$-means, we show a convergence rate of $\Omega\left(\sqrt{\frac{kj}{n}}\right)$ is necessary, thereby proving that the bounds from [Fefferman, Mitter, and Narayanan, Journal of the Mathematical Society 2016] are essentially optimal.
翻译:暂无翻译