An entropy stable spectral vanishing viscosity for discontinuous Galerkin schemes: application to shock capturing and LES models

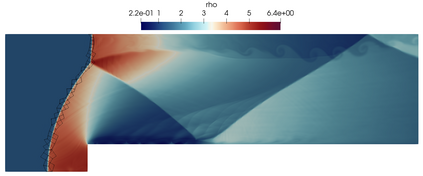
We present a stable spectral vanishing viscosity for discontinuous Galerkin schemes, with applications to turbulent and supersonic flows. The idea behind the SVV is to spatially filter the dissipative fluxes, such that it concentrates in higher wavenumbers, where the flow is typically under-resolved, leaving low wavenumbers dissipation-free. Moreover, we derive a stable approximation of the Guermond-Popov fluxes with the Bassi-Rebay 1 scheme, used to introduce density regularization in shock capturing simulations. This filtering uses a Cholesky decomposition of the fluxes that ensures the entropy stability of the scheme, which also includes a stable approximation of boundary conditions for adiabatic walls. For turbulent flows, we test the method with the three-dimensional Taylor-Green vortex and show that energy is correctly dissipated, and the scheme is stable when a kinetic energy preserving split-form is used in combination with a low dissipation Riemann solver. Finally, we test the shock capturing capabilities of our method with the Shu-Osher and the supersonic forward facing step cases, obtaining good results without spurious oscillations even with coarse meshes.