Graphical Evidence

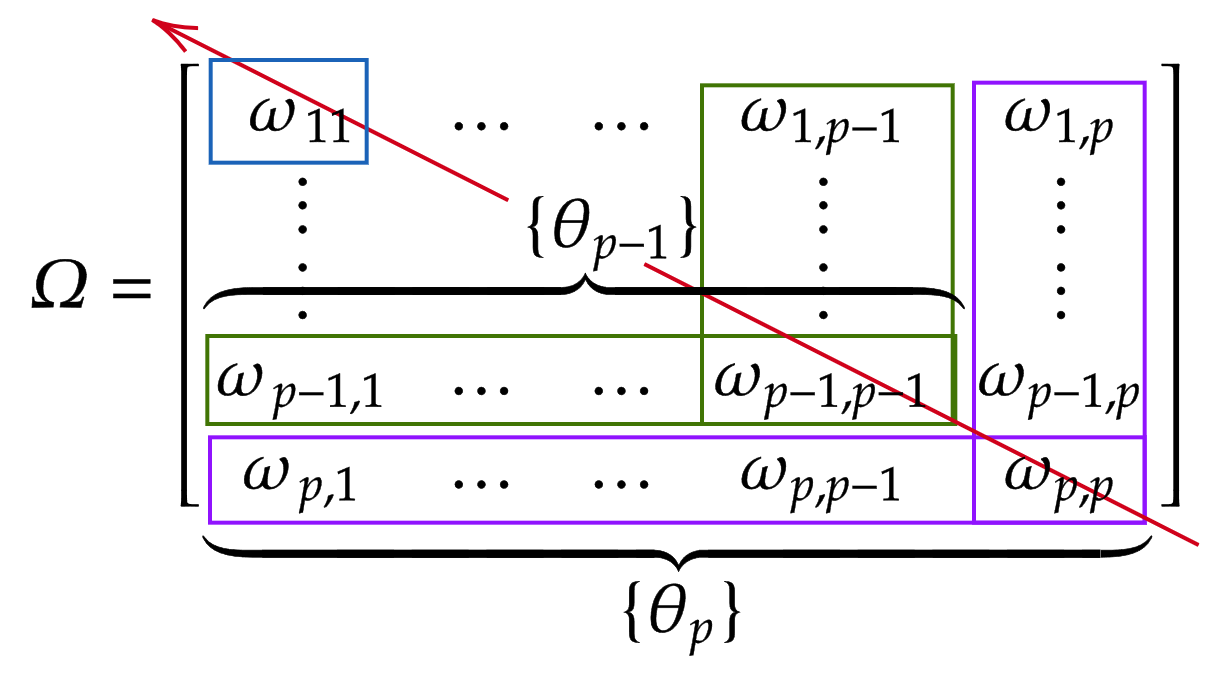
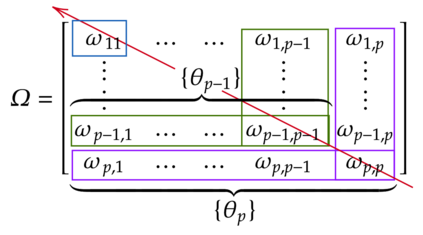
Marginal likelihood, also known as model evidence, is a fundamental quantity in Bayesian statistics. It is used for model selection using Bayes factors or for empirical Bayes tuning of prior hyper-parameters. Yet, the calculation of evidence has remained a longstanding open problem in Gaussian graphical models. Currently, the only feasible solutions that exist are for special cases such as the Wishart or G-Wishart, in moderate dimensions. We present an application of Chib's technique that is applicable to a very broad class of priors under mild requirements. Specifically, the requirements are: (a) the priors on the diagonal terms on the precision matrix can be written as gamma or scale mixtures of gamma random variables and (b) those on the off-diagonal terms can be represented as normal or scale mixtures of normal. This includes structured priors such as the Wishart or G-Wishart, and more recently introduced element-wise priors, such as the Bayesian graphical lasso and the graphical horseshoe. Among these, the true marginal is known in an analytically closed form for Wishart, providing a useful validation of our approach. For the general setting of the other three, and several more priors satisfying conditions (a) and (b) above, the calculation of evidence has remained an open question that this article seeks to resolve.