Analysis and Numerical Approximation of Stationary Second-Order Mean Field Game Partial Differential Inclusions

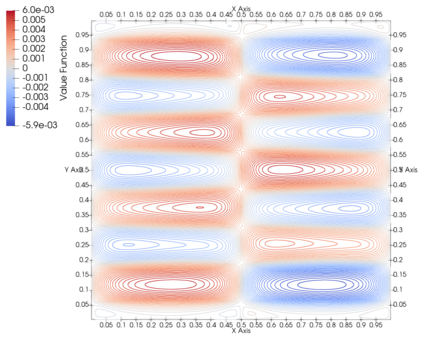
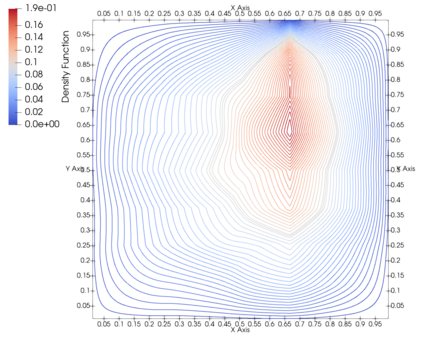
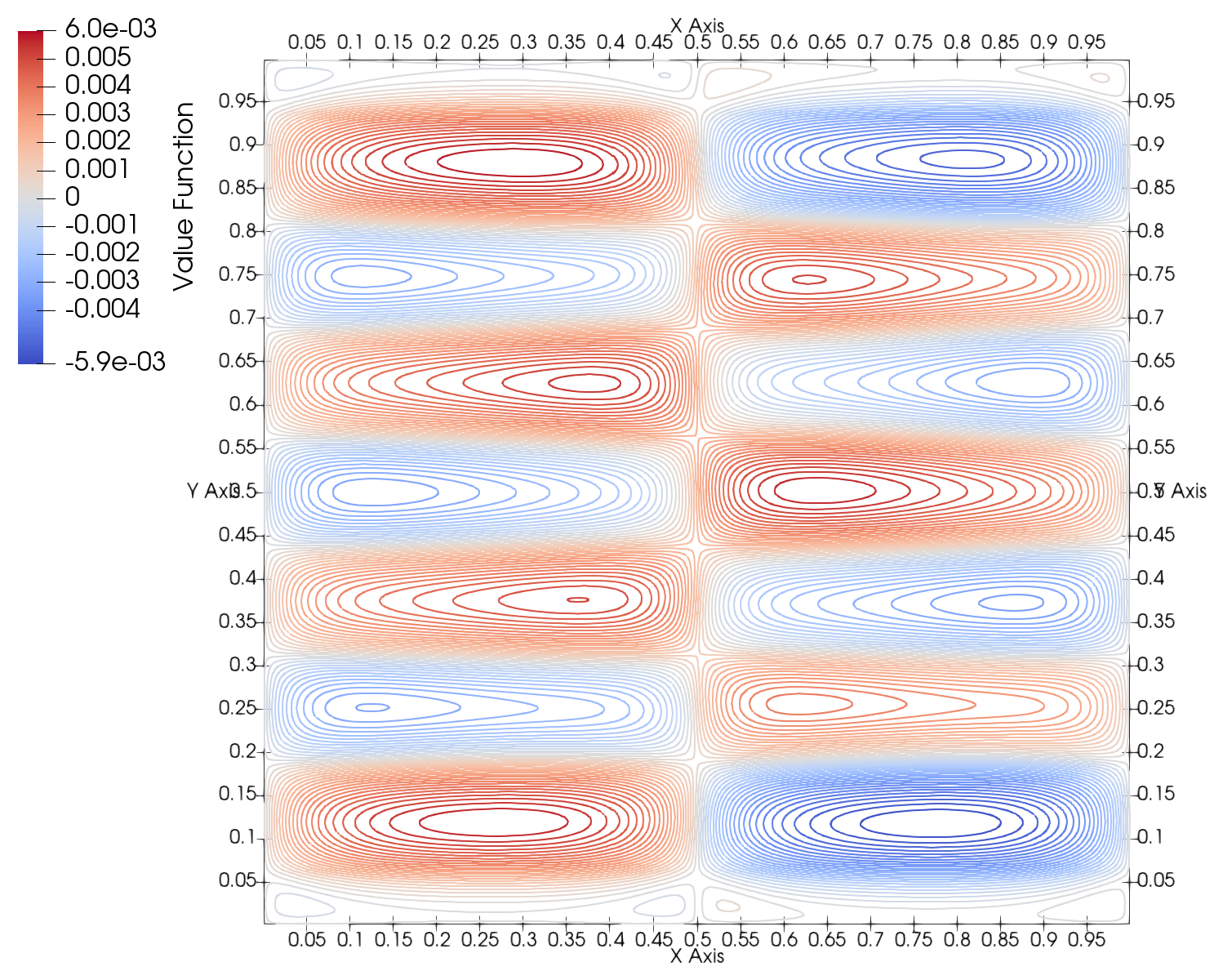
The formulation of Mean Field Games (MFG) typically requires continuous differentiability of the Hamiltonian in order to determine the advective term in the Kolmogorov--Fokker--Planck equation for the density of players. However in many cases of practical interest, the underlying optimal control problem may exhibit bang-bang controls, which typically lead to nondifferentiable Hamiltonians. We develop the analysis and numerical analysis of stationary MFG for the general case of convex, Lipschitz, but possibly nondifferentiable Hamiltonians. In particular, we propose a generalization of the MFG system as a Partial Differential Inclusion (PDI) based on interpreting the derivative of the Hamiltonian in terms of subdifferentials of convex functions. We establish existence of a weak solution to the MFG PDI system, and we further prove uniqueness under a similar monotonicity condition to the one considered by Lasry and Lions. We then propose a monotone finite element discretization of the problem, and we prove strong $H^1$-norm convergence of the approximations to the value function and strong $L^q$-norm convergence of the approximations of the density function. We illustrate the performance of the numerical method in numerical experiments featuring nonsmooth solutions.