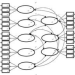
Discovering cause-effect relationships between variables from observational data is a fundamental challenge in many scientific disciplines. However, in many situations it is desirable to directly estimate the change in causal relationships across two different conditions, e.g., estimating the change in genetic expression across healthy and diseased subjects can help isolate genetic factors behind the disease. This paper focuses on the problem of directly estimating the structural difference between two structural equation models (SEMs), having the same topological ordering, given two sets of samples drawn from the individual SEMs. We present an principled algorithm that can recover the difference SEM in $\mathcal{O}(d^2 \log p)$ samples, where $d$ is related to the number of edges in the difference SEM of $p$ nodes. We also study the fundamental limits and show that any method requires at least $\Omega(d' \log \frac{p}{d'})$ samples to learn difference SEMs with at most $d'$ parents per node. Finally, we validate our theoretical results with synthetic experiments and show that our method outperforms the state-of-the-art. Moreover, we show the usefulness of our method by using data from the medical domain.
翻译:从观测数据中发现变量之间的因果关系是许多科学学科的一项根本挑战。然而,在许多情况下,直接估计两种不同条件下因果关系的变化是可取的,例如,估计健康和疾病对象的遗传表达方式的变化可以帮助分离疾病背后的遗传因素。本文侧重于直接估计两种结构方程模型(SEMs)之间的结构差异的问题,两种结构方程的顺序相同,具有相同的地貌顺序,从单个的SEM中取出两组样本。我们提出了一个原则性算法,可以恢复在$\mathca{O}(d%2\log p) 和美元样本中的SEM差异。在这两种不同条件下,直接估计因果关系的变化是可取的,例如,估计健康和疾病主体的基因表达方式的变化有助于分离出疾病背后的遗传因素。我们还研究了基本限度,并表明任何方法都需要至少$\Omega(d) (d)\log\frac{p ⁇ d} 样本来学习SEMEMEM的差别。最后,我们用合成实验来验证我们的理论结果,并表明我们的方法从医学领域显示我们所使用的方法。