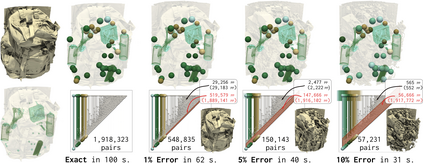
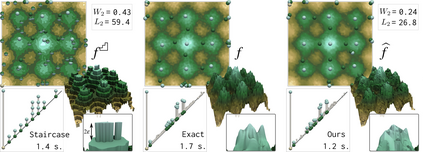
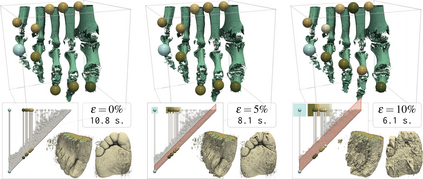
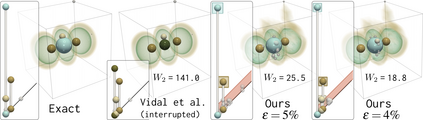
This paper presents an algorithm for the efficient approximation of the saddle-extremum persistence diagram of a scalar field. Vidal et al. introduced recently a fast algorithm for such an approximation (by interrupting a progressive computation framework). However, no theoretical guarantee was provided regarding its approximation quality. In this work, we revisit the progressive framework of Vidal et al. and we introduce in contrast a novel approximation algorithm, with a user controlled approximation error, specifically, on the Bottleneck distance to the exact solution. Our approach is based on a hierarchical representation of the input data, and relies on local simplifications of the scalar field to accelerate the computation, while maintaining a controlled bound on the output error. The locality of our approach enables further speedups thanks to shared memory parallelism. Experiments conducted on real life datasets show that for a mild error tolerance (5% relative Bottleneck distance), our approach improves runtime performance by 18% on average (and up to 48% on large, noisy datasets) in comparison to standard, exact, publicly available implementations. In addition to the strong guarantees on its approximation error, we show that our algorithm also provides in practice outputs which are on average 5 times more accurate (in terms of the L2-Wasserstein distance) than a naive approximation baseline. We illustrate the utility of our approach for interactive data exploration and we document visualization strategies for conveying the uncertainty related to our approximations.
翻译:本文展示了使马鞍- Expremum 持续性图表快速近似的一个算法 。 Vidal 等人最近推出了一个快速算法, 以加速计算。 但是, 我们没有就其近似质量提供理论保证 。 在这项工作中, 我们重新审视Vidal et al. 的进步框架, 我们引入了一个新的近似算法, 使用用户控制的近似差错, 具体来说, 具体来说, 在输入数据与精确解决方案之间的距离上, 我们的方法以输入数据的等级代表为基础, 并依靠对卡路里域的本地简化来加速计算, 同时保持对输出错误的受控约束。 我们方法的地理位置使得由于共享记忆平行关系而能够进一步加速。 在实际生活数据集上进行的实验表明,为了温和的错误容忍度( 5% 相对Bottleneck 距离), 我们的方法比标准、 准确的、 准确的数据集提高了运行时间的18%( 48% ), 并依靠可公开得到的执行。 除了对其精确误差的精确的校准计算外, 我们的方法还展示了我们的直观文件的精确度数据。