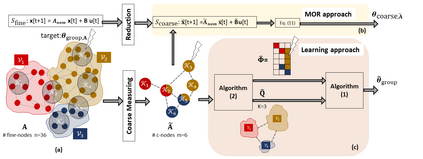
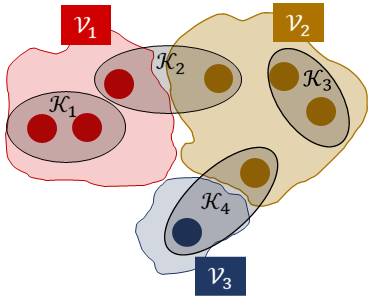
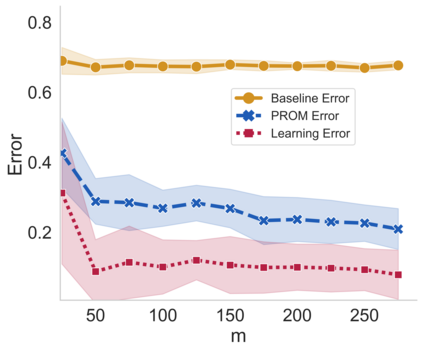
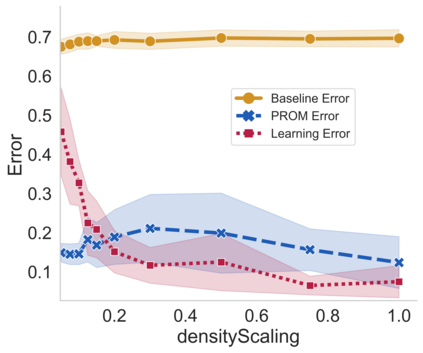
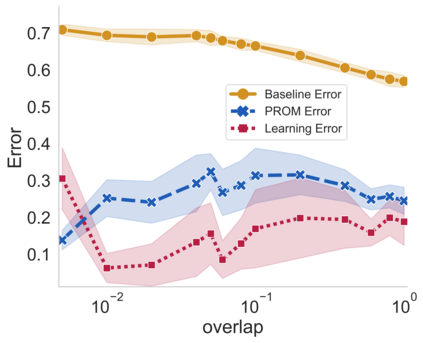
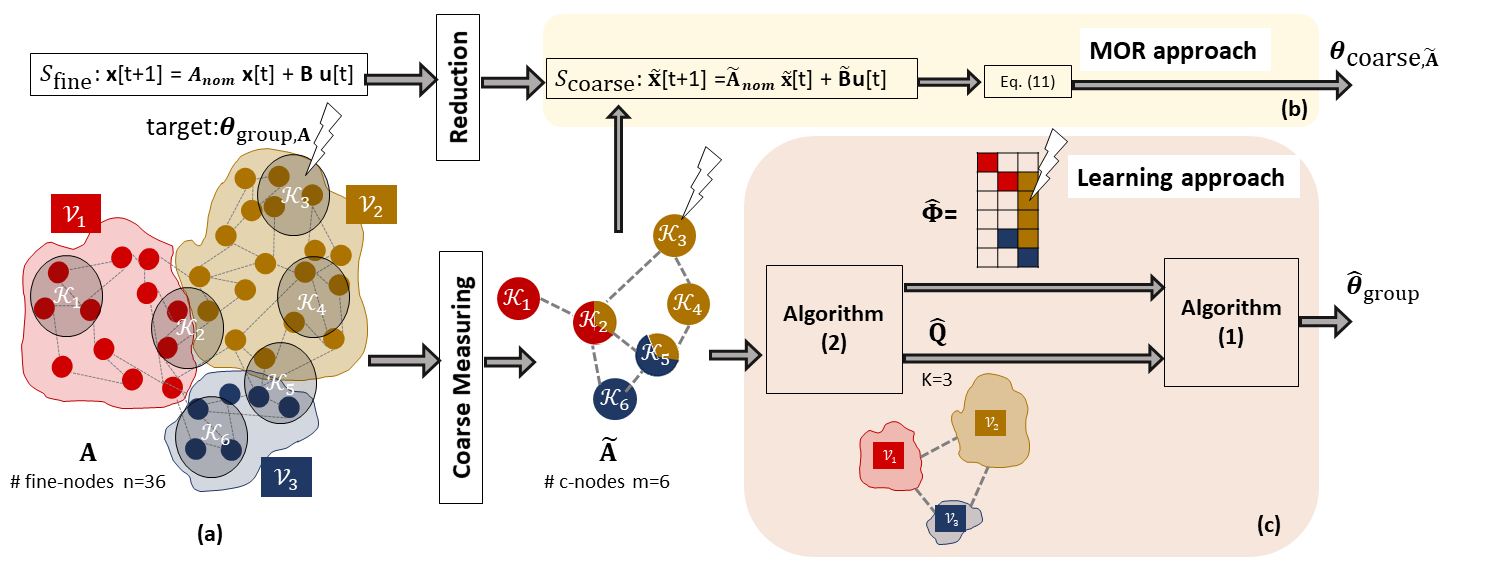
We consider the controllability of large-scale linear networked dynamical systems when complete knowledge of network structure is unavailable and knowledge is limited to coarse summaries. We provide conditions under which average controllability of the fine-scale system can be well approximated by average controllability of the (synthesized, reduced-order) coarse-scale system. To this end, we require knowledge of some inherent parametric structure of the fine-scale network that makes this type of approximation possible. Therefore, we assume that the underlying fine-scale network is generated by the stochastic block model (SBM) -- often studied in community detection. We then provide an algorithm that directly estimates the average controllability of the fine-scale system using a coarse summary of SBM. Our analysis indicates the necessity of underlying structure (e.g., in-built communities) to be able to quantify accurately the controllability from coarsely characterized networked dynamics. We also compare our method to that of the reduced-order method and highlight the regimes where both can outperform each other. Finally, we provide simulations to confirm our theoretical results for different scalings of network size and density, and the parameter that captures how much community-structure is retained in the coarse summary.
翻译:我们认为,当对网络结构的完整知识缺乏,而知识仅限于粗略摘要时,大规模线性网络动态系统的可控性是大型线性网络式动态系统的可控性。我们提供了一种条件,使微规模系统的平均可控性能够被(合成的、缩序的)粗略系统的平均可控性大致接近于(合成的、缩序的)粗略系统的可控性。为此,我们要求了解微规模网络的某些固有的可控性结构,使这种类型的近似成为可能。因此,我们假定基本的微规模网络是由随机区块模型(SBM)生成的(SBM) -- -- 通常在社区探测中研究的。我们然后提供一种算法,直接估计微规模系统的平均可控性,使用微缩的SBM系统粗略的概要。我们的分析表明,基本结构(例如,内部的社区)必须能够准确量化粗度的网络型动态的可控性。我们还将我们的方法与减序式方法进行比较,并突出两者的系统。最后,我们提供模拟,以证实我们所保留的网络结构结构的理论结果如何精确地测量网络密度和共同测量。