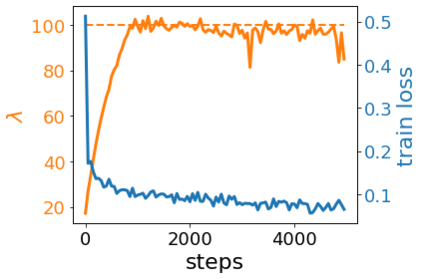
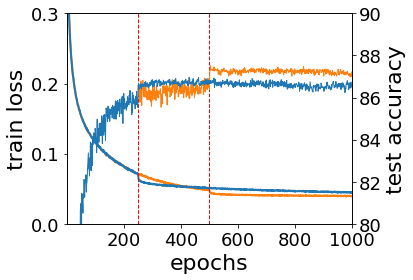
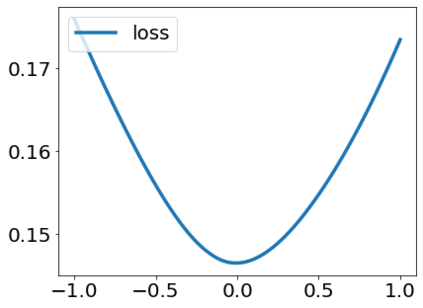
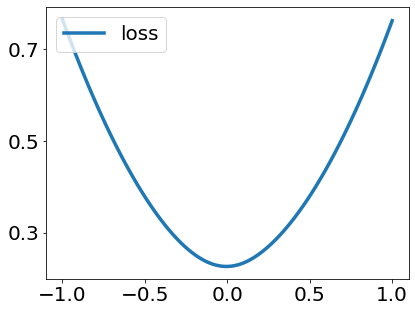
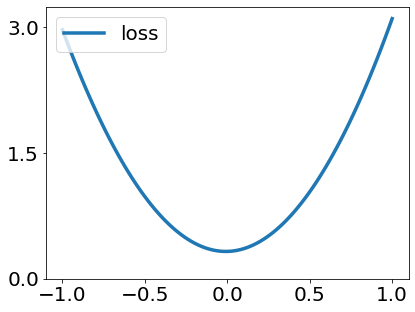
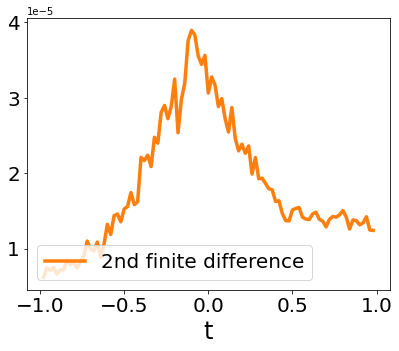
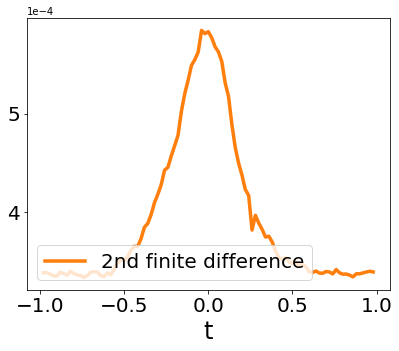
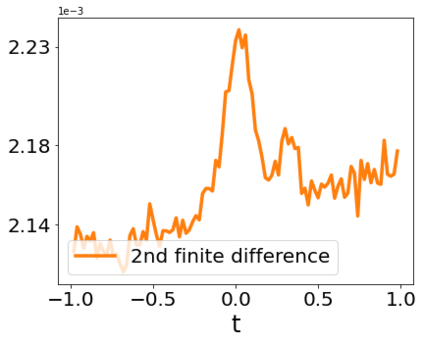
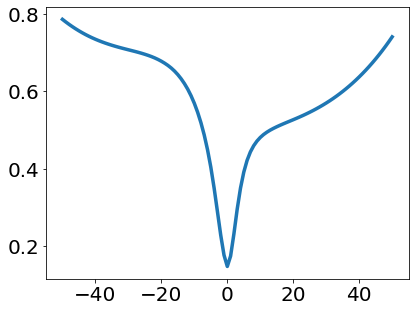
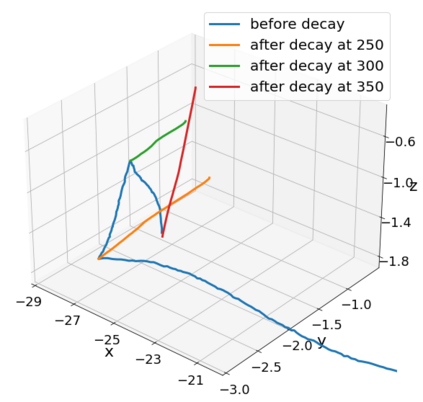
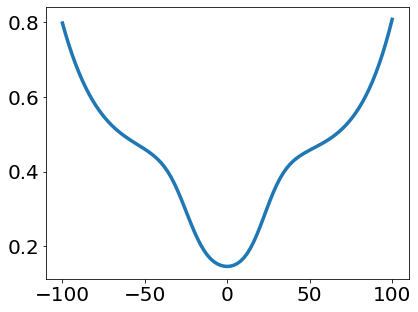
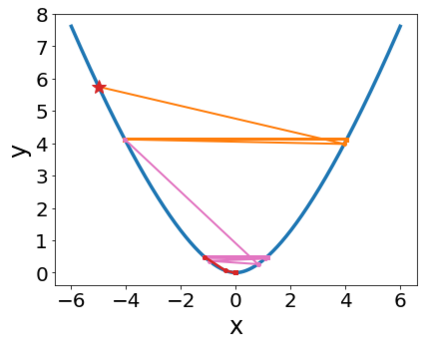
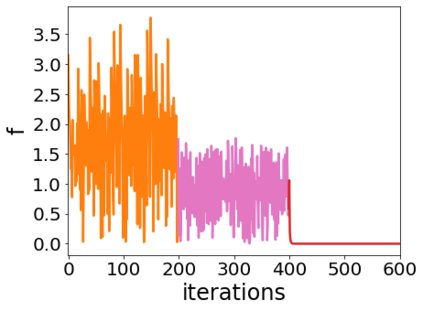
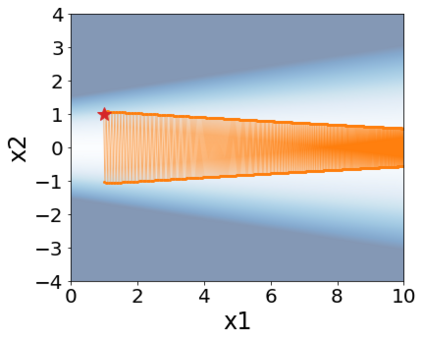
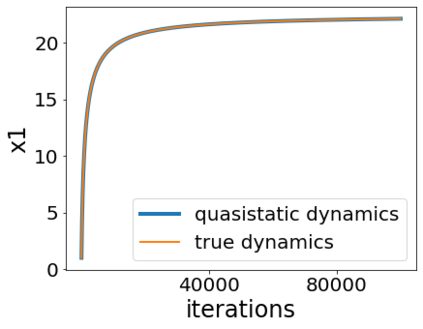
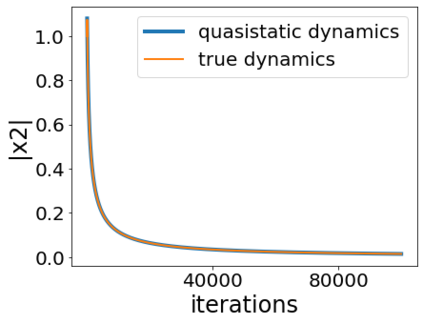
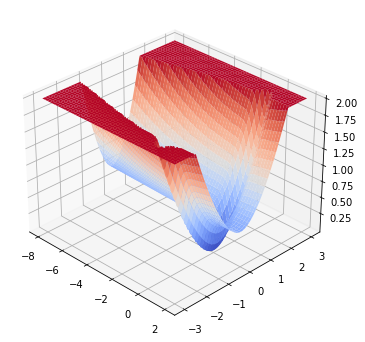
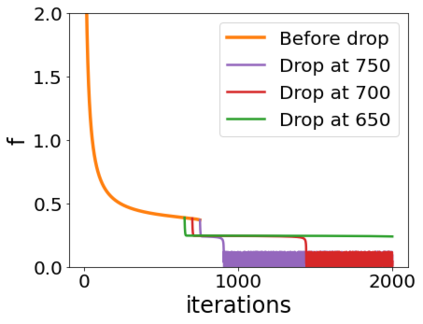
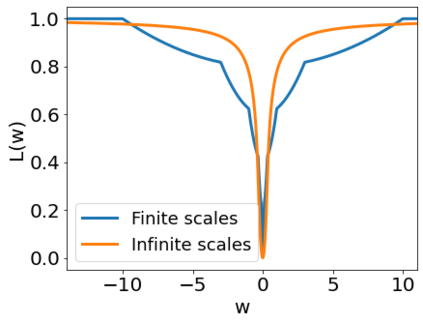
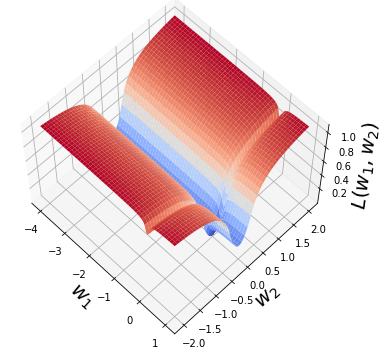
A quadratic approximation of neural network loss landscapes has been extensively used to study the optimization process of these networks. Though, it usually holds in a very small neighborhood of the minimum, it cannot explain many phenomena observed during the optimization process. In this work, we study the structure of neural network loss functions and its implication on optimization in a region beyond the reach of a good quadratic approximation. Numerically, we observe that neural network loss functions possesses a multiscale structure, manifested in two ways: (1) in a neighborhood of minima, the loss mixes a continuum of scales and grows subquadratically, and (2) in a larger region, the loss shows several separate scales clearly. Using the subquadratic growth, we are able to explain the Edge of Stability phenomenon [5] observed for the gradient descent (GD) method. Using the separate scales, we explain the working mechanism of learning rate decay by simple examples. Finally, we study the origin of the multiscale structure and propose that the non-convexity of the models and the non-uniformity of training data is one of the causes. By constructing a two-layer neural network problem we show that training data with different magnitudes give rise to different scales of the loss function, producing subquadratic growth and multiple separate scales.
翻译:大量使用神经网络损失表面的二次近似度来研究这些网络的优化过程。 虽然通常在极小的一小块区域中, 它无法解释优化过程中观察到的许多现象。 在这项工作中, 我们研究神经网络损失功能的结构及其对在一个良好的二次近距离所无法达到的区域优化的影响。 从数字上看, 我们观察到神经网络损失功能具有一个多尺度的结构, 表现在两种方式:(1) 在微型附近, 损失混合着一个尺度的连续体, 并生长在次赤道区域, (2) 在更大的区域, 损失明显显示几个不同的尺度。 利用亚赤道增长, 我们能够解释为梯度下坡度(GD)方法观测到的稳定现象[5] 。 我们用不同的尺度来解释学习率衰减的工作机制。 最后, 我们研究多尺度结构的起源, 并提议模型的不一致性和不统一性是造成这些原因之一。 通过构建一个两层神经网络的分级结构, 我们用不同尺度来显示不同层次的神经网络的升幅, 我们用不同的尺度来显示数据显示不同层次的升幅。