Tensor Moments of Gaussian Mixture Models: Theory and Applications

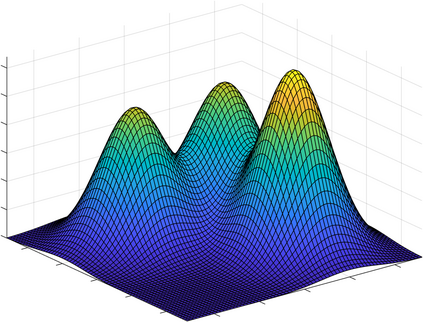
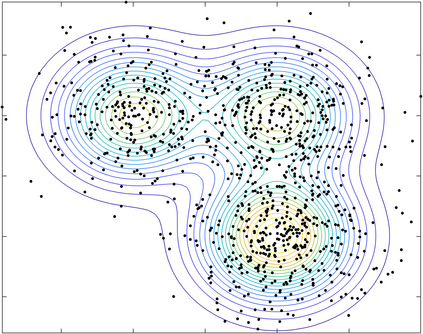
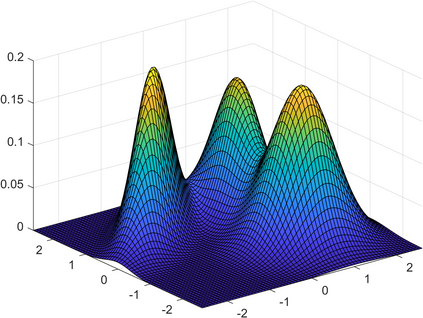
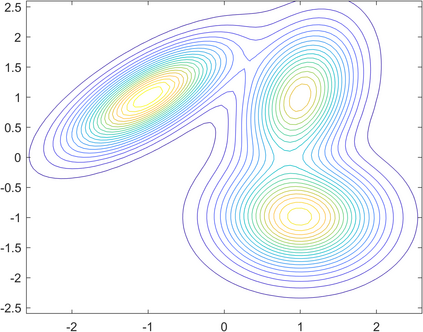
Gaussian mixture models (GMM) are fundamental tools in statistical and data sciences. We study the moments of multivariate Gaussians and GMMs. The $d$-th moment of an $n$-dimensional random variable is a symmetric $d$-way tensor of size $n^d$, so working with moments naively is assumed to be prohibitively expensive for $d>2$ and larger values of $n$. In this work, we develop theory and numerical methods for implicit computations with moment tensors of GMMs, reducing the computational and storage costs to $\mathcal{O}(n^2)$ and $\mathcal{O}(n^3)$, respectively, for general covariance matrices, and to $\mathcal{O}(n)$ and $\mathcal{O}(n)$, respectively, for diagonal ones. We derive concise analytic expressions for the moments in terms of symmetrized tensor products, relying on the correspondence between symmetric tensors and homogeneous polynomials, and combinatorial identities involving Bell polynomials. The primary application of this theory is to estimating GMM parameters from a set of observations, when formulated as a moment-matching optimization problem. If there is a known and common covariance matrix, we also show it is possible to debias the data observations, in which case the problem of estimating the unknown means reduces to symmetric CP tensor decomposition. Numerical results validate and illustrate the numerical efficiency of our approaches. This work potentially opens the door to the competitiveness of the method of moments as compared to expectation maximization methods for parameter estimation of GMMs.