The Exact Asymptotic Form of Bayesian Generalization Error in Latent Dirichlet Allocation

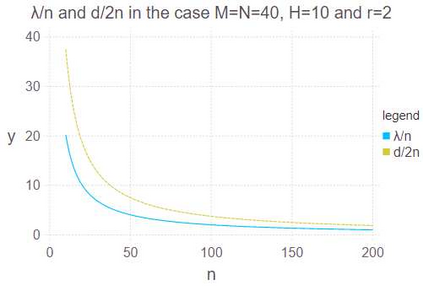
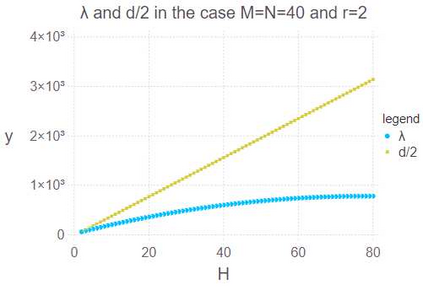
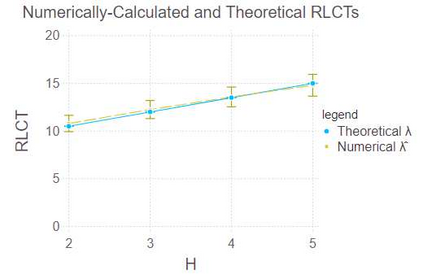
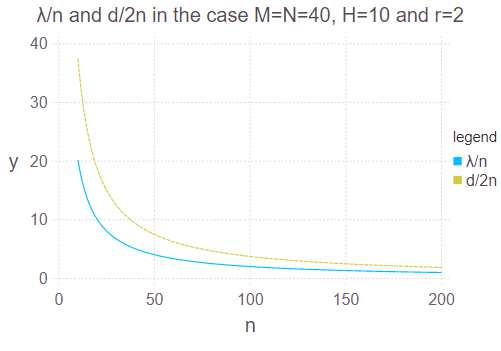
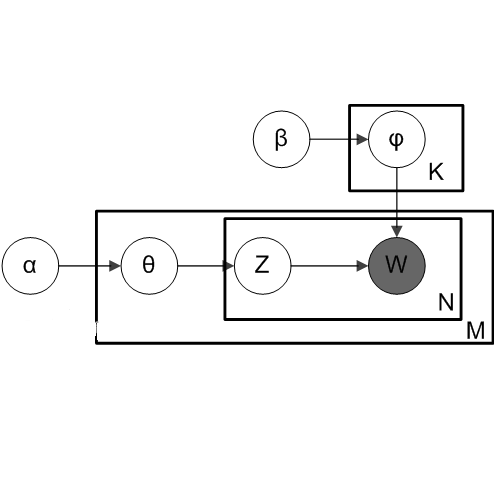
Latent Dirichlet allocation (LDA) obtains essential information from data by using Bayesian inference. It is applied to knowledge discovery via dimension reducing and clustering in many fields. However, its generalization error had not been yet clarified since it is a singular statistical model where there is no one-to-one mapping from parameters to probability distributions. In this paper, we give the exact asymptotic form of its generalization error and marginal likelihood, by theoretical analysis of its learning coefficient using algebraic geometry. The theoretical result shows that the Bayesian generalization error in LDA is expressed in terms of that in matrix factorization and a penalty from the simplex restriction of LDA's parameter region. A numerical experiment is consistent to the theoretical result.