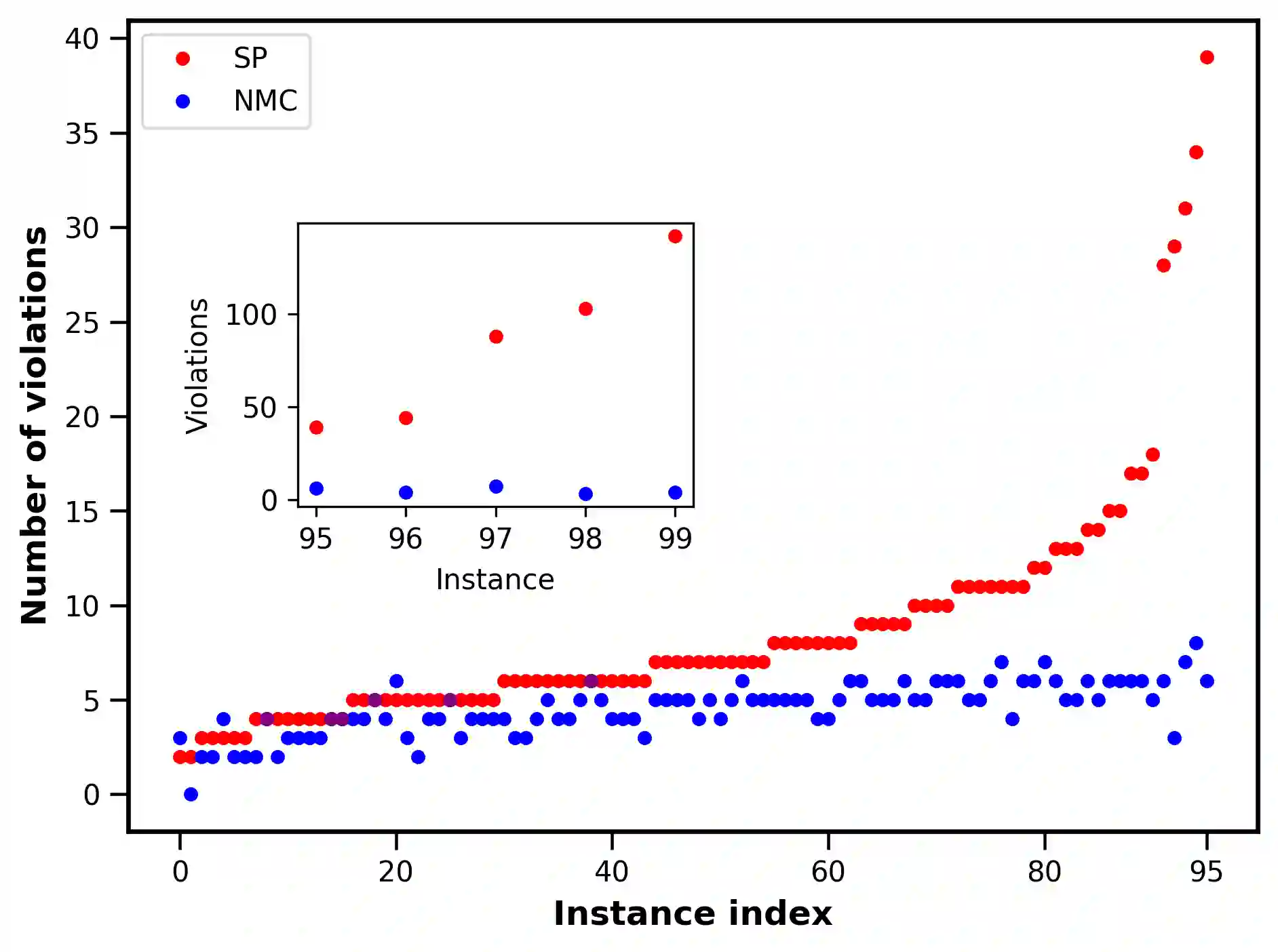
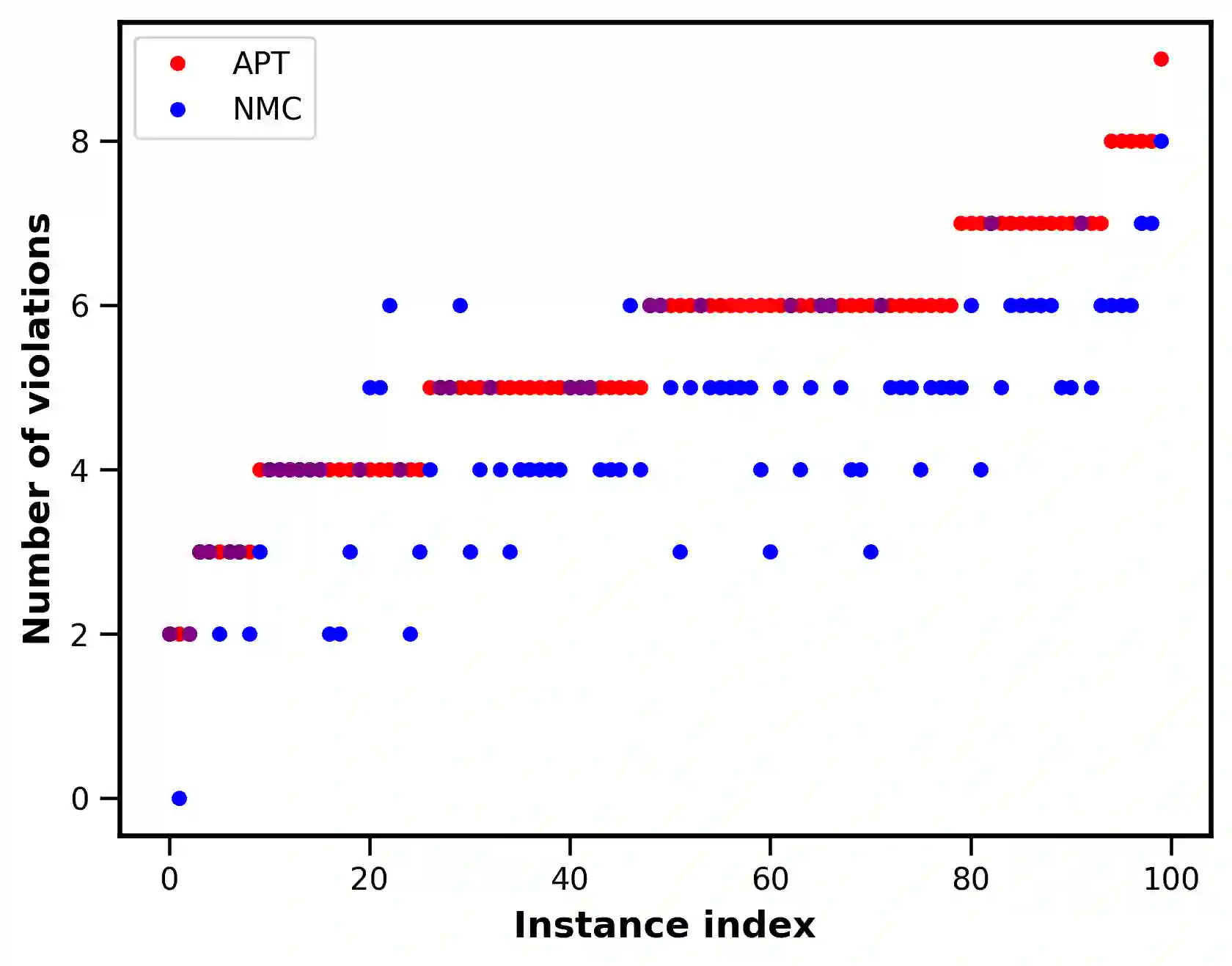
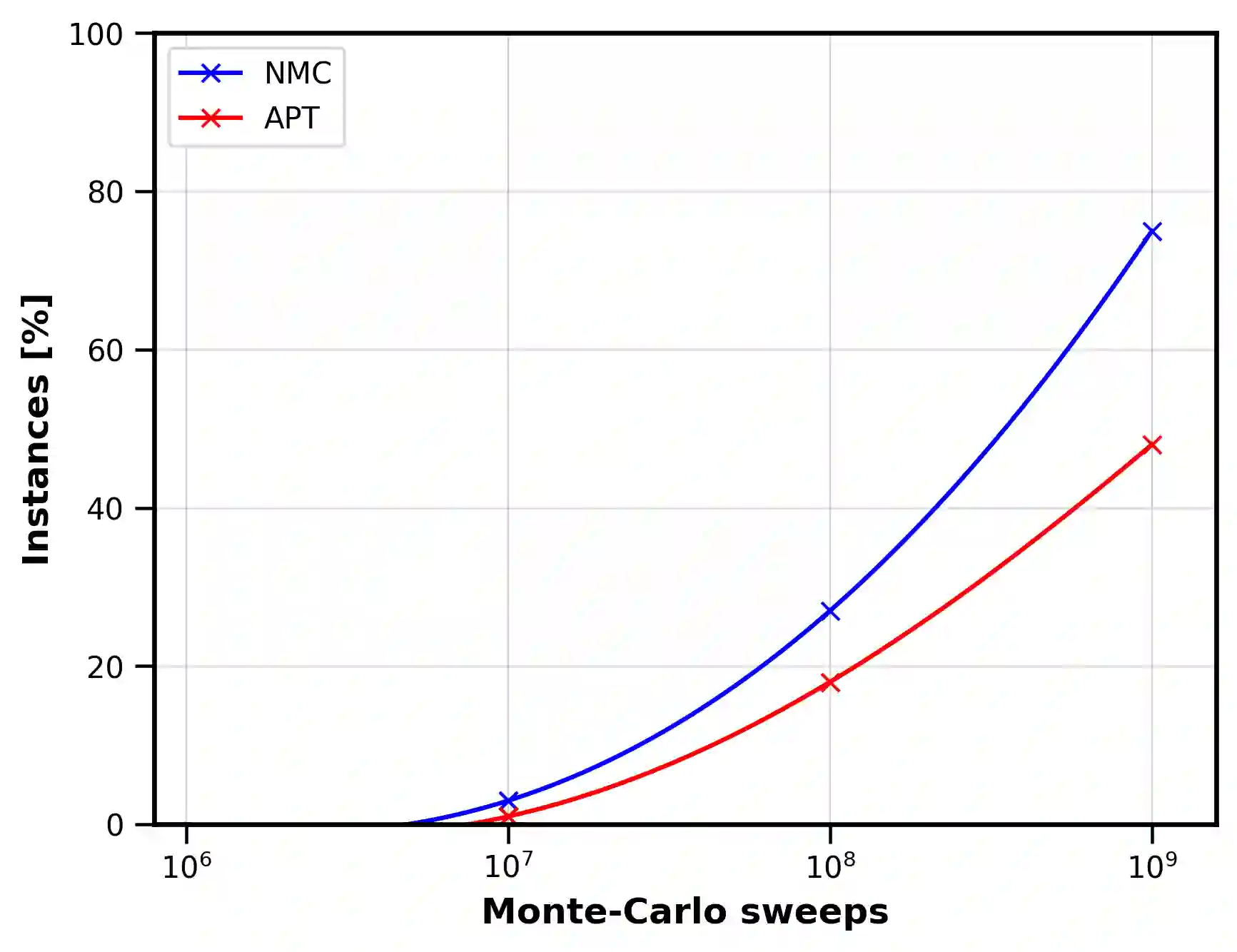
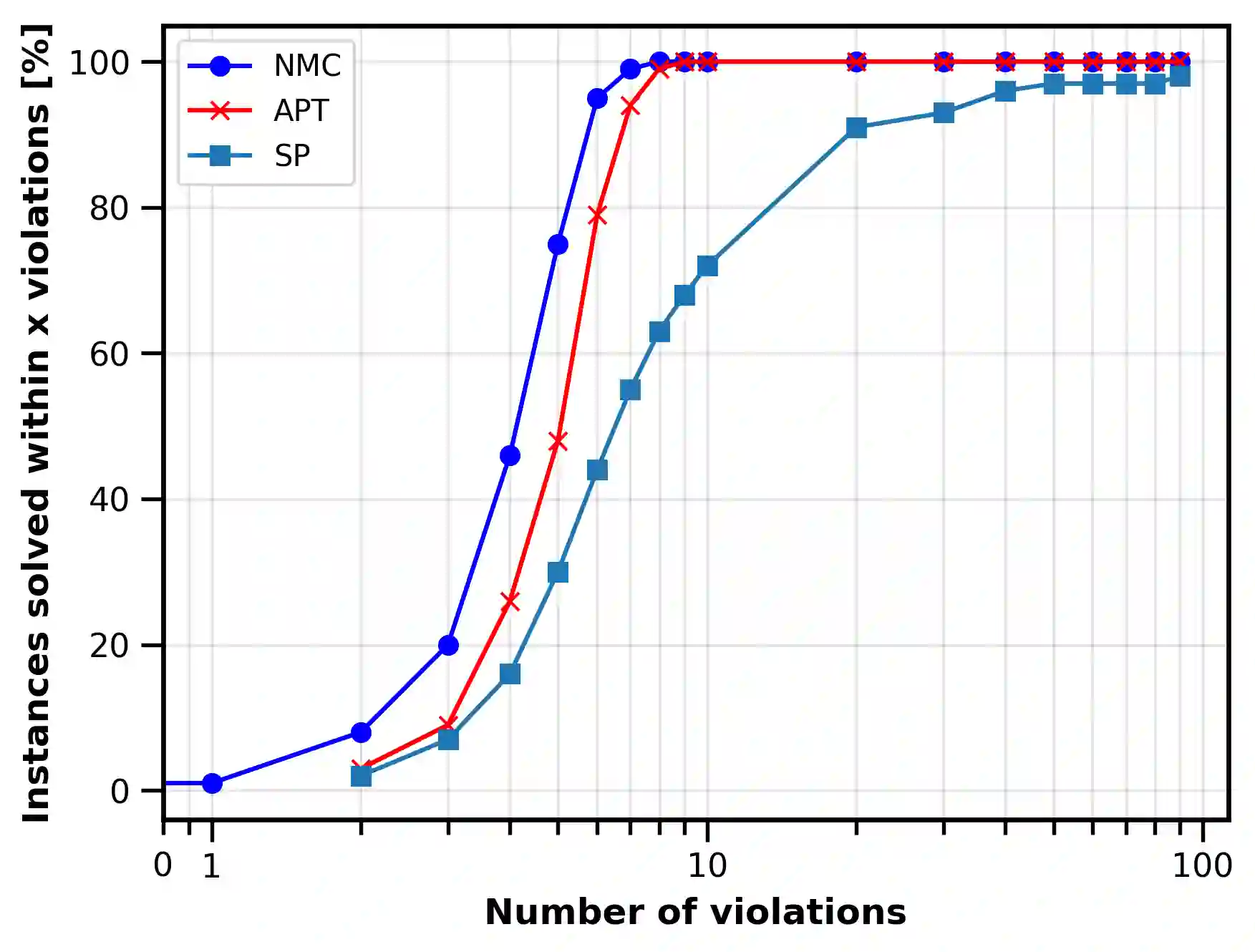
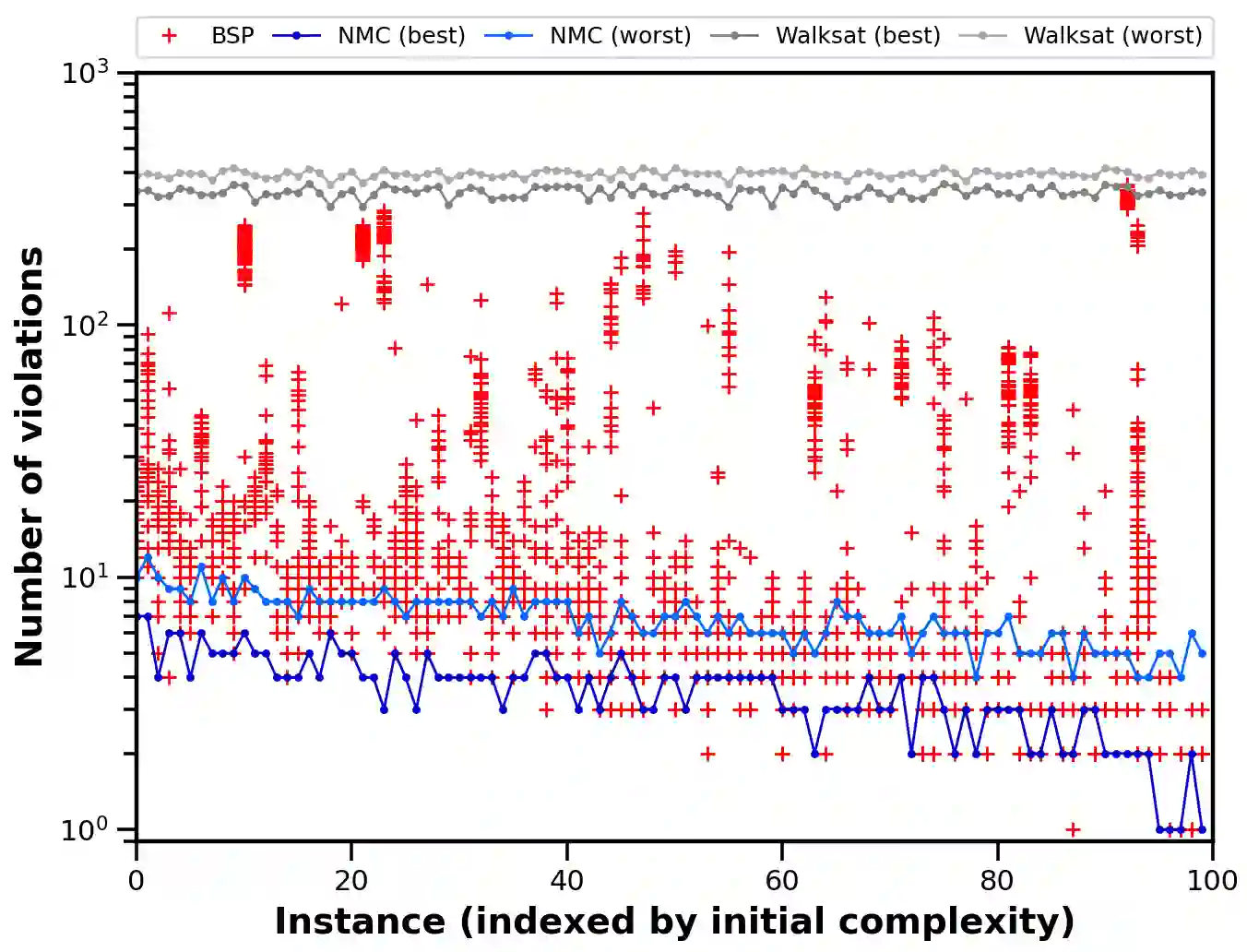
Optimizing highly complex cost/energy functions over discrete variables is at the heart of many open problems across different scientific disciplines and industries. A major obstacle is the emergence of many-body effects among certain subsets of variables in hard instances leading to critical slowing down or collective freezing for known stochastic local search strategies. An exponential computational effort is generally required to unfreeze such variables and explore other unseen regions of the configuration space. Here, we introduce a quantum-inspired family of nonlocal Nonequilibrium Monte Carlo (NMC) algorithms by developing an adaptive gradient-free strategy that can efficiently learn key instance-wise geometrical features of the cost function. That information is employed on-the-fly to construct spatially inhomogeneous thermal fluctuations for collectively unfreezing variables at various length scales, circumventing costly exploration versus exploitation trade-offs. We apply our algorithm to two of the most challenging combinatorial optimization problems: random k-satisfiability (k-SAT) near the computational phase transitions and Quadratic Assignment Problems (QAP). We observe significant speedup and robustness over both specialized deterministic solvers and generic stochastic solvers. In particular, for 90% of random 4-SAT instances we find solutions that are inaccessible for the best specialized deterministic algorithm known as Survey Propagation (SP) with an order of magnitude improvement in the quality of solutions for the hardest 10% instances. We also demonstrate two orders of magnitude improvement in time-to-solution over the state-of-the-art generic stochastic solver known as Adaptive Parallel Tempering (APT).
翻译:在离散的变量上优化高度复杂的成本/能源功能是不同科学学科和行业许多程度的公开问题的核心所在。一个主要障碍是,在困难情况下,某些子类变量中出现许多体形效应,导致已知的随机本地搜索战略出现严重减慢或集体冻结。通常需要指数计算努力来解冻这些变量并探索配置空间的其他隐蔽区域。在这里,我们通过制定适应性梯度的无梯度计算法,从而能够有效地学习成本函数中关键实例的几何性特征。信息在飞行中被用于构建空间性不均匀的热波动,以在不同的长度范围内集体解冻变量,绕过昂贵的勘探和开发交易。我们运用我们的算法来应对两个最具挑战性的组合优化问题:在计算阶段附近的宽度平衡(k-SAT)算法(k-SAT),通过制定适应性梯度的升级法改进方法(QAP),我们观测到在标准化的中,在标准化的中,在标准化的慢度-萨洛特-萨洛特-萨洛特-卡(Scrmal-comlistal-ral-comlist)中,我们所知道的10个最难解解的解的解的解的路径中,也是特定的10个特定的解算。