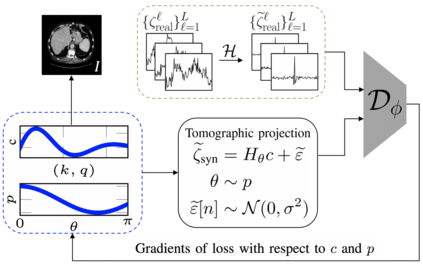
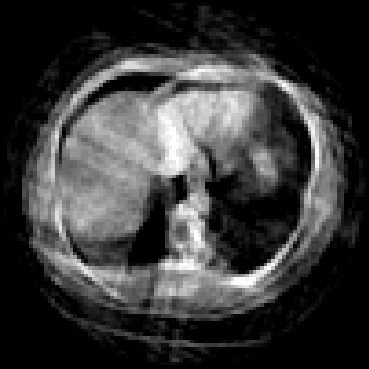
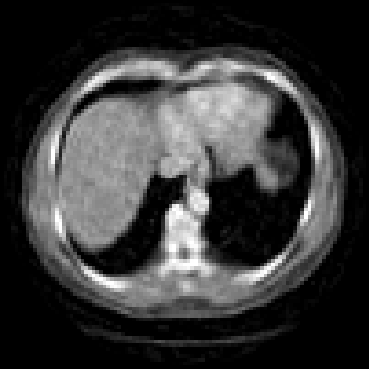
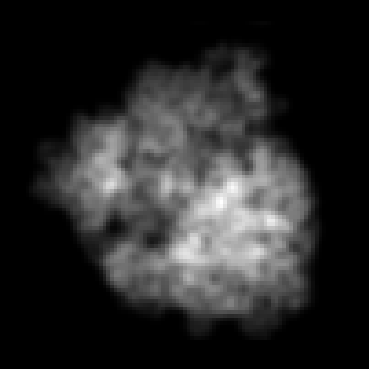
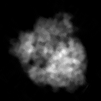
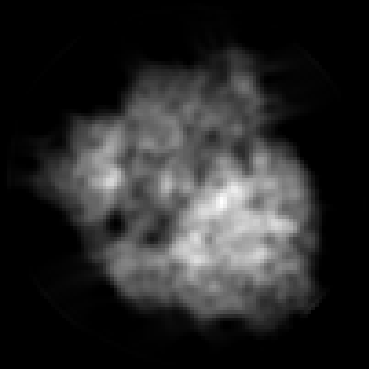
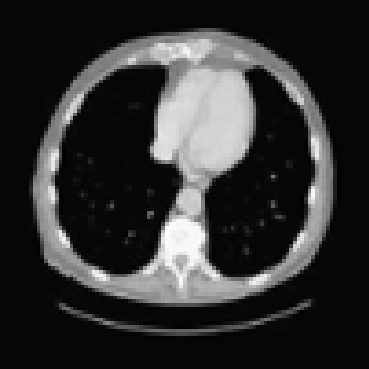
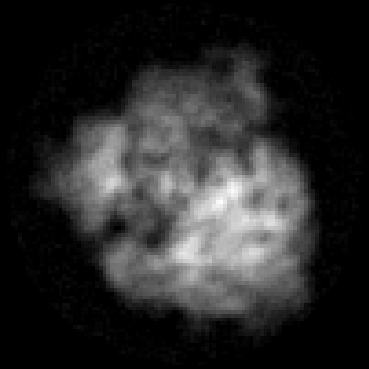
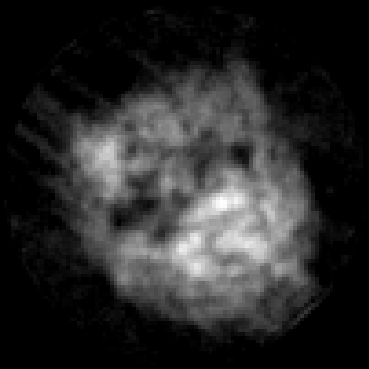
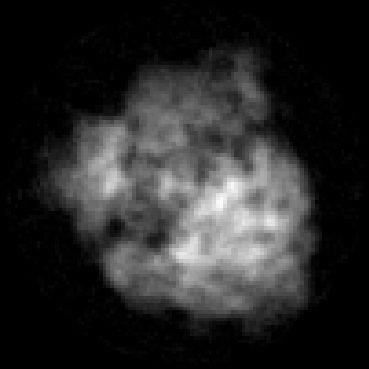
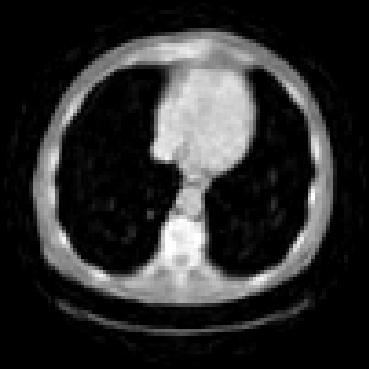
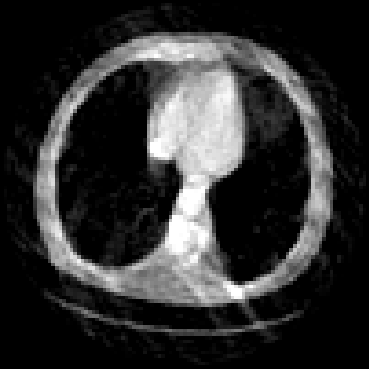
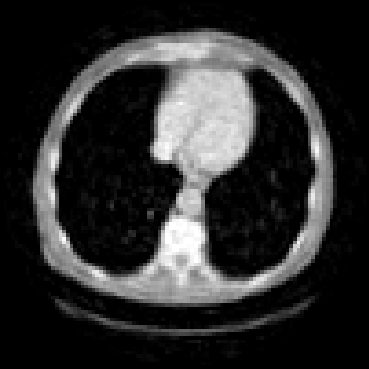
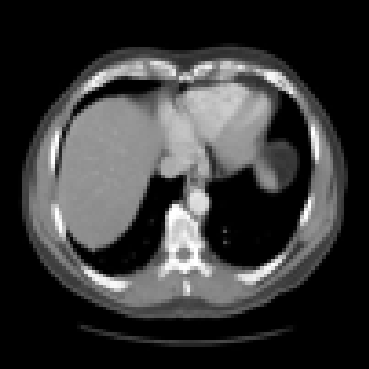
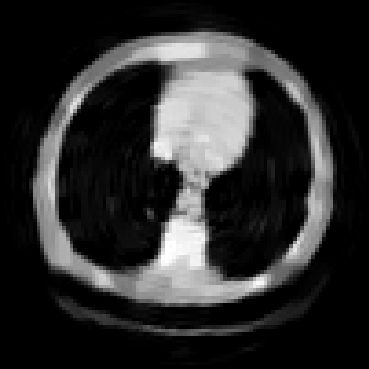
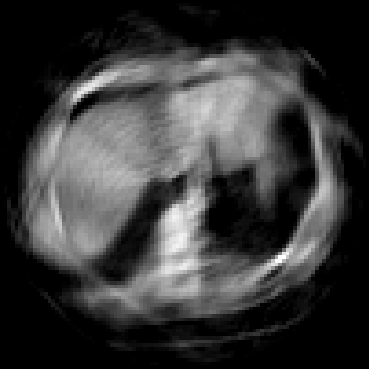
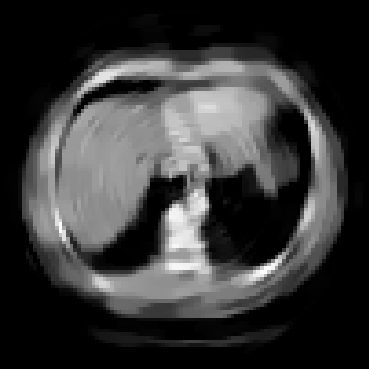
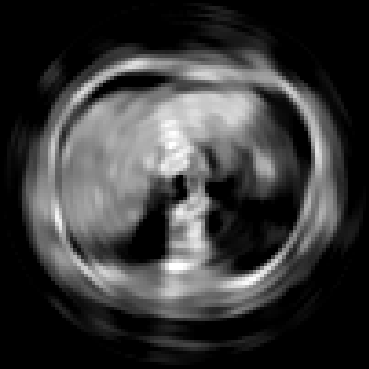
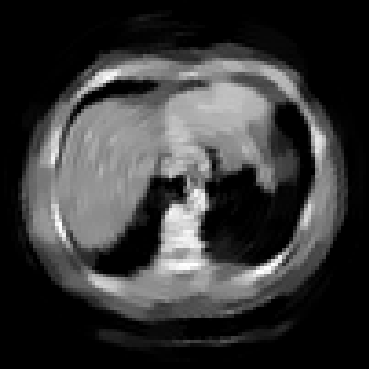
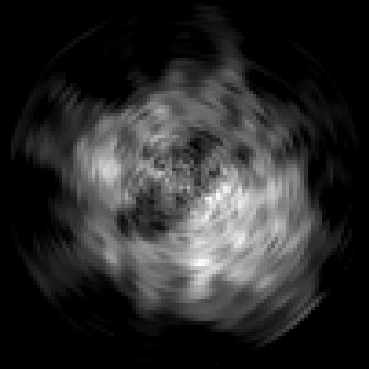
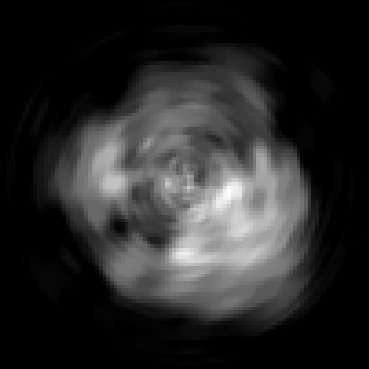
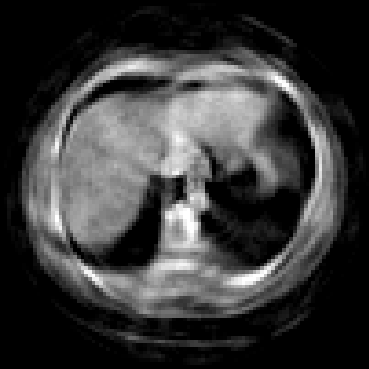
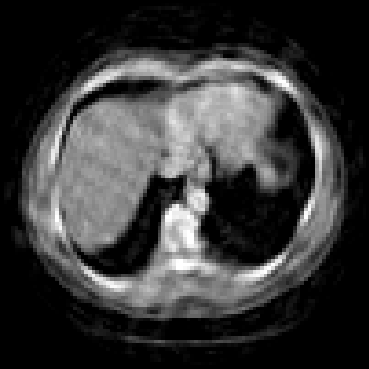
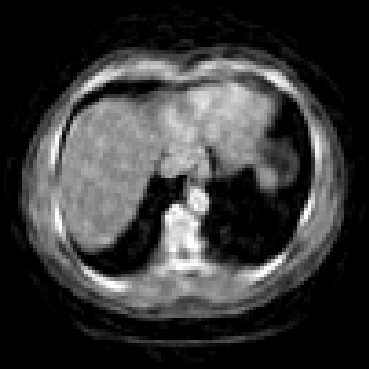
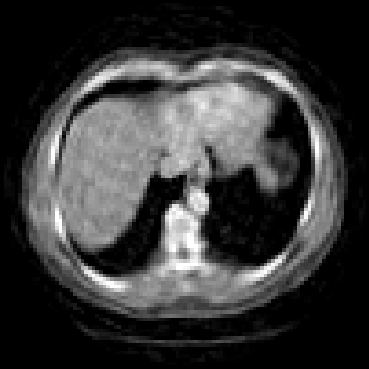
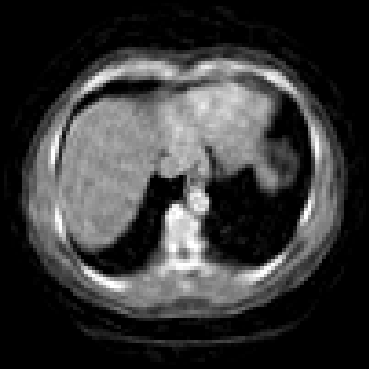
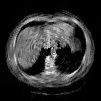
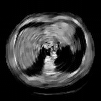
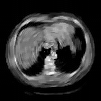
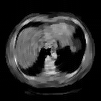
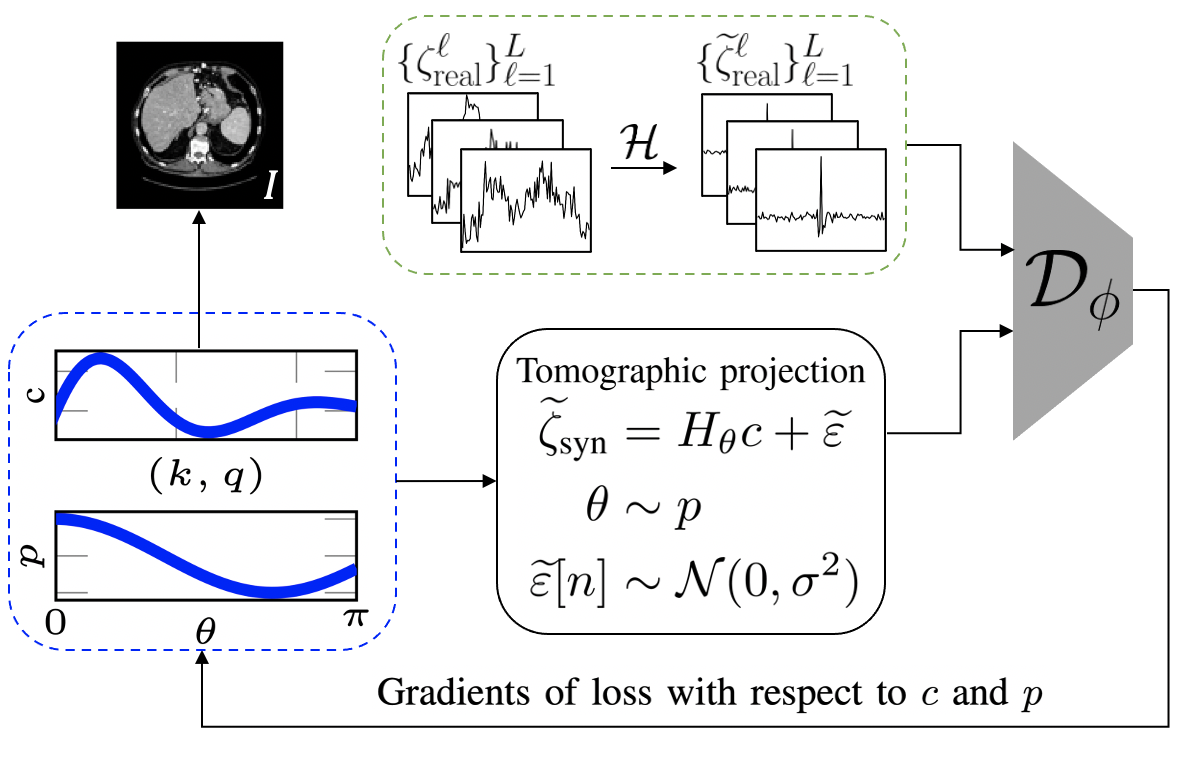
The goal of 2D tomographic reconstruction is to recover an image given its projections from various views. It is often presumed that projection angles associated with the projections are known in advance. Under certain situations, however, these angles are known only approximately or are completely unknown. It becomes more challenging to reconstruct the image from a collection of random projections. We propose an adversarial learning based approach to recover the image and the projection angle distribution by matching the empirical distribution of the measurements with the generated data. Fitting the distributions is achieved through solving a min-max game between a generator and a critic based on Wasserstein generative adversarial network structure. To accommodate the update of the projection angle distribution through gradient back propagation, we approximate the loss using the Gumbel-Softmax reparameterization of samples from discrete distributions. Our theoretical analysis verifies the unique recovery of the image and the projection distribution up to a rotation and reflection upon convergence. Our extensive numerical experiments showcase the potential of our method to accurately recover the image and the projection angle distribution under noise contamination.
翻译:2D 映像重建的目标是从各种观点的预测中恢复图像,通常假定与预测有关的投影角度是事先已知的。但是,在某些情况下,这些角度只大致为人所知或完全不为人知。从随机投影的集合中重建图像更具挑战性。我们提议以对抗性学习为基础,通过将测量结果的实证分布与生成的数据相匹配,恢复图像和投影角分布。通过解决基于瓦森斯坦基因对抗网络结构的发电机和评论家之间的微轴游戏,实现分布。为了适应通过梯度反传播更新投影角度分布的情况,我们用离散分布样本的甘贝尔-软轴重新校准来估计损失。我们的理论分析核实了图像的独特恢复以及预测分布,然后在聚合后进行旋转和反省。我们广泛的数字实验展示了我们方法在噪音污染下准确恢复图像和投影角度分布的潜力。