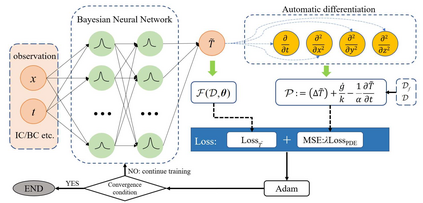
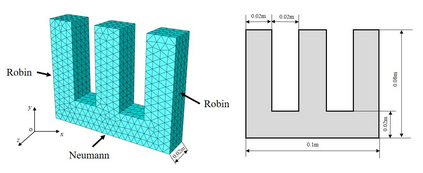
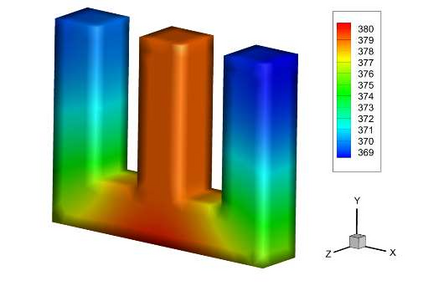
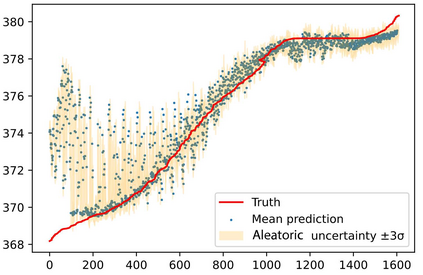
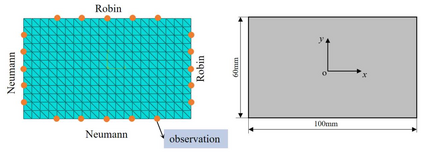
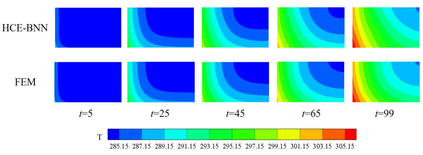
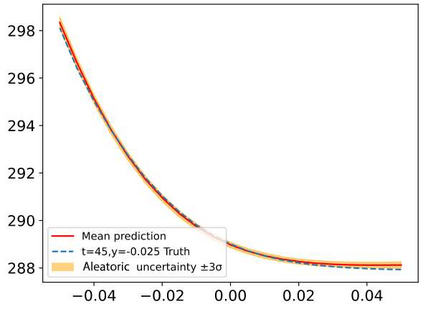
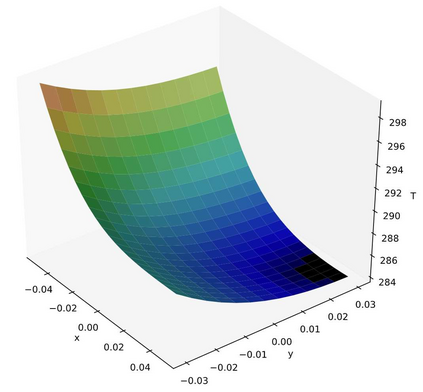
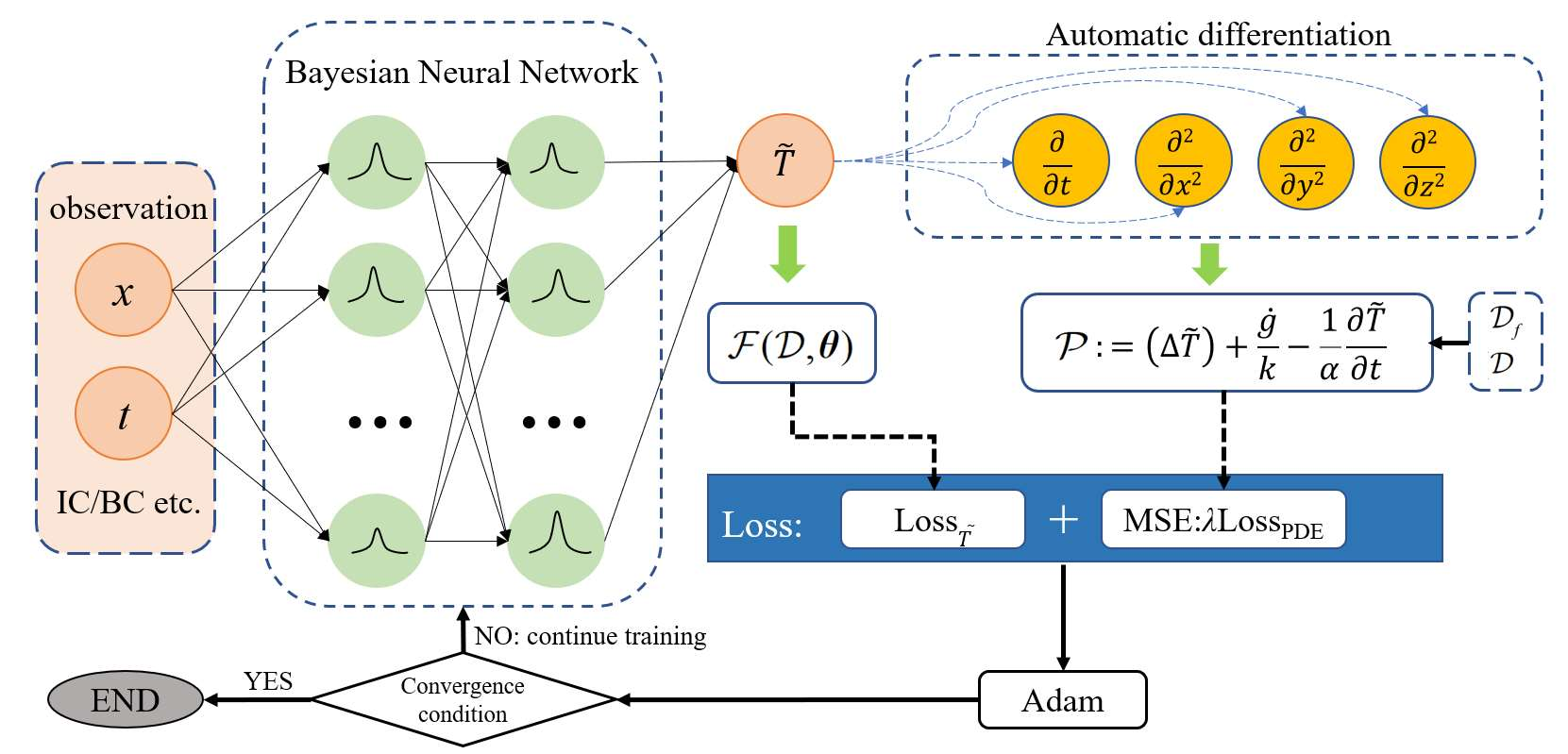
In this study, a novel physics-data-driven Bayesian method named Heat Conduction Equation assisted Bayesian Neural Network (HCE-BNN) is proposed. The HCE-BNN is constructed based on the Bayesian neural network, it is a physics-informed machine learning strategy. Compared with the existed pure data driven method, to acquire physical consistency and better performance of the data-driven model, the heat conduction equation is embedded into the loss function of the HCE-BNN as a regularization term. Hence, the proposed method can build a more reliable model by physical constraints with less data. The HCE-BNN can handle the forward and inverse problems consistently, that is, to infer unknown responses from known partial responses, or to identify boundary conditions or material parameters from known responses. Compared with the exact results, the test results demonstrate that the proposed method can be applied to both heat conduction forward and inverse problems successfully. In addition, the proposed method can be implemented with the noisy data and gives the corresponding uncertainty quantification for the solutions.
翻译:在这项研究中,提出了一种新型物理学-数据驱动的贝叶斯人热操控赤道辅助巴伊西亚神经网络(HCE-BNN)的新方法。HCE-BNN是根据拜伊斯神经网络建造的,这是一种了解物理学的机器学习战略。与现有的纯数据驱动方法相比,为了获得数据驱动模型的实际一致性和更好的性能,热操控方程式作为一个正规术语嵌入了HCE-BNN的损失功能。因此,拟议的方法可以通过物理限制和较少的数据建立一个更可靠的模型。HCE-BNN可以一贯地处理前向和反向问题,即从已知的部分反应中推断出未知的反应,或从已知反应中确定边界条件或物质参数。与确切的结果相比,试验结果表明,拟议的方法既可以适用于前向的热导,也可以成功地适用于反向的问题。此外,拟议的方法可以与噪音数据一起实施,并对解决办法提供相应的不确定性量化。