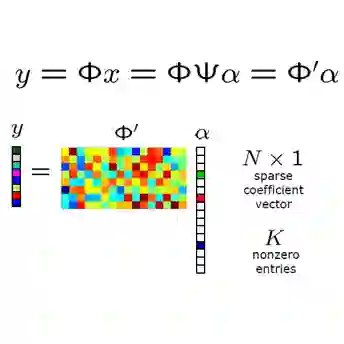
In underwater acoustics, shallow water environments act as modal dispersive waveguides when considering low-frequency sources. In this context, propagating signals can be described as a sum of few modal components, each of them propagating according to its own wavenumber. Estimating these wavenumbers is of key interest to understand the propagating environment as well as the emitting source. To solve this problem, we proposed recently a Bayesian approach exploiting a sparsity-inforcing prior. When dealing with broadband sources, this model can be further improved by integrating the particular dependence linking the wavenumbers from one frequency to the other. In this contribution, we propose to resort to a new approach relying on a restricted Boltzmann machine, exploited as a generic structured sparsity-inforcing model. This model, derived from deep Bayesian networks, can indeed be efficiently learned on physically realistic simulated data using well-known and proven algorithms.
翻译:在水下声学中,浅水环境在考虑低频源时充当模式分散波导。 在这方面,可把传播信号描述为几个模式组件的总和,每个模式组件都按其本身的波号进行传播。估计这些波数对于了解传播环境以及排放源至关重要。为了解决这个问题,我们最近提议了一种巴伊西亚方法,利用先前的孔径渗透。在处理宽带源时,可以通过整合将波数从一个频率连接到另一个频率的特定依赖性来进一步改进这一模型。在这个贡献中,我们提议采用一种新的方法,依靠一种有限的波尔兹曼机器,作为通用结构松散型信息模型加以利用。这一模型来自深巴伊西亚网络,确实能够有效地从使用众所周知和经过验证的算法的符合实际现实的模拟数据中学习。