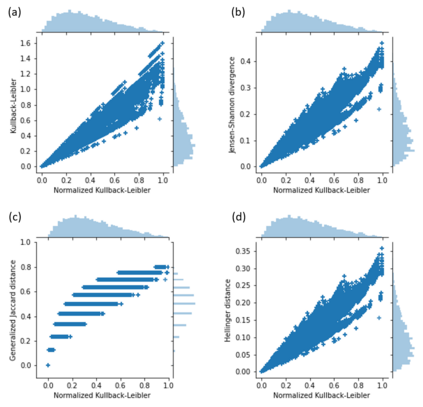
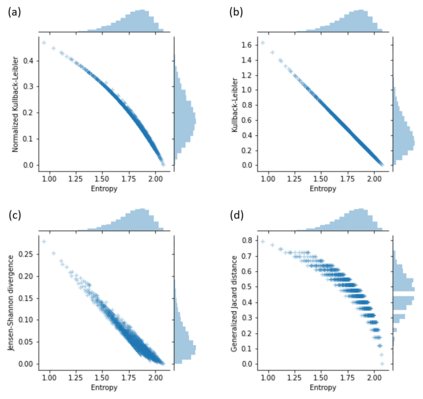
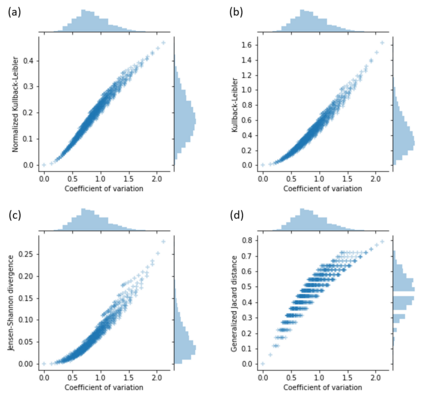
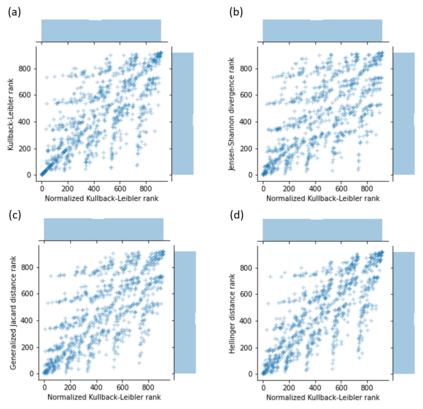
This work presents an upper-bound to value that the Kullback-Leibler (KL) divergence can reach for a class of probability distributions called quantum distributions (QD). The aim is to find a distribution $U$ which maximizes the KL divergence from a given distribution $P$ under the assumption that $P$ and $U$ have been generated by distributing a given discrete quantity, a quantum. Quantum distributions naturally represent a wide range of probability distributions that are used in practical applications. Moreover, such a class of distributions can be obtained as an approximation of any probability distribution. The retrieving of an upper-bound for the entropic divergence is here shown to be possible under the condition that the compared distributions are quantum distributions over the same quantum value, thus they become comparable. Thus, entropic divergence acquires a more powerful meaning when it is applied to comparable distributions. This aspect should be taken into account in future developments of divergences. The theoretical findings are used for proposing a notion of normalized KL divergence that is empirically shown to behave differently from already known measures.
翻译:这项工作呈现出一个上限值值, 即 Kullback- Leiber (KL) 差值对于被称为量子分布(QD) 的概率分布类别可能达到的值值值值。 目的是找到一个分配值美元, 使 KL 与给定分配值P美元的差异最大化, 前提是分配量( 量子) 和 美元是通过分配给定的离散数量( 量子) 产生的。 量子分布自然代表了实际应用中所使用的各种概率分布。 此外, 这种分配值类别可以作为任何概率分布的近似值获得。 这里显示, 在比较分配量分布为同一量值的量分布量分布因而变得可比的条件下, 收回一个上限值差异是可能的。 因此, 当对可比较的分布值应用到可比较的分布量值时, 则获得更强烈的含义。 这个问题应该在今后的差异发展中加以考虑。 理论结论用于提出一个标准化的 KL差值概念, 其经验表明, 与已知的措施不同。