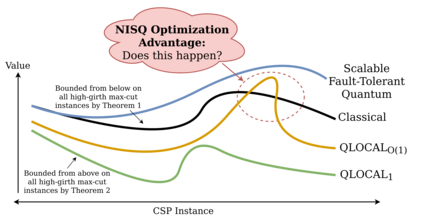
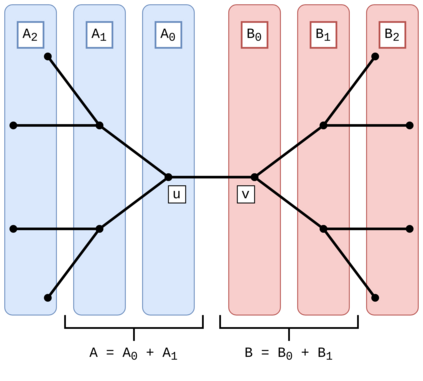
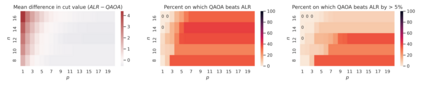
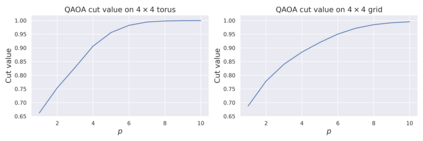
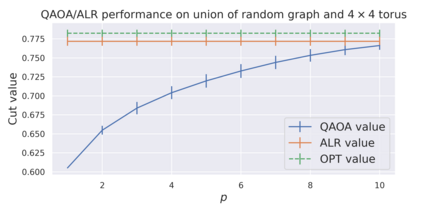
We study the performance of local quantum algorithms such as the Quantum Approximate Optimization Algorithm (QAOA) for the maximum cut problem, and their relationship to that of classical algorithms. (1) We prove that every (quantum or classical) one-local algorithm achieves on $D$-regular graphs of girth $> 5$ a maximum cut of at most $1/2 + C/\sqrt{D}$ for $C=1/\sqrt{2} \approx 0.7071$. This is the first such result showing that one-local algorithms achieve a value bounded away from the true optimum for random graphs, which is $1/2 + P_*/\sqrt{D} + o(1/\sqrt{D})$ for $P_* \approx 0.7632$. (2) We show that there is a classical $k$-local algorithm that achieves a value of $1/2 + C/\sqrt{D} - O(1/\sqrt{k})$ for $D$-regular graphs of girth $> 2k+1$, where $C = 2/\pi \approx 0.6366$. This is an algorithmic version of the existential bound of Lyons and is related to the algorithm of Aizenman, Lebowitz, and Ruelle (ALR) for the Sherrington-Kirkpatrick model. This bound is better than that achieved by the one-local and two-local versions of QAOA on high-girth graphs. (3) Through computational experiments, we give evidence that the ALR algorithm achieves better performance than constant-locality QAOA for random $D$-regular graphs, as well as other natural instances, including graphs that do have short cycles. Our experimental work suggests that it could be possible to extend beyond our theoretical constraints. This points at the tantalizing possibility that $O(1)$-local quantum maximum-cut algorithms might be *pointwise dominated* by polynomial-time classical algorithms, in the sense that there is a classical algorithm outputting cuts of equal or better quality *on every possible instance*. This is in contrast to the evidence that polynomial-time algorithms cannot simulate the probability distributions induced by local quantum algorithms.
翻译:我们研究了本地量子算法的性能,例如用于最大截断问题的Qaintum Apress 优化算法(QAOA),以及它们与古典算法的关系。 (1) 我们证明每个(Qaantum或古典)一地算法都能用美元(美元)的常规图形以美元=5美元最多削减1/2 + C/\qrt{D}美元。 (2) 我们显示,对于美元=1/\ sqrt{2}\ approdalalalal 算法来说,美元=1/2 + Crtrick=0.071美元。这是第一个这样的结果,显示一地算算算算算法(QA1-roral dismology) 的值与真正的随机图表(美元+P ⁇ /\\\\\ sqrrt{D}+美元(美元) 美元/美元)的正常运算法(美元/美元/美元/美元)的货币运算法(Oral_美元/美元/美元)