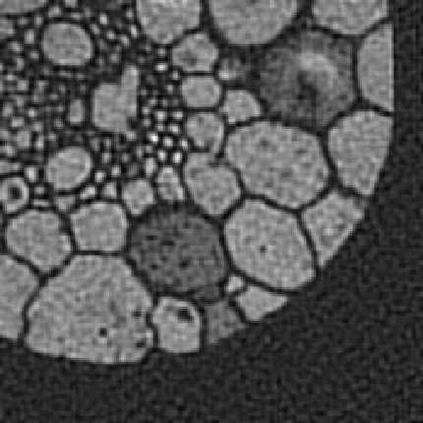
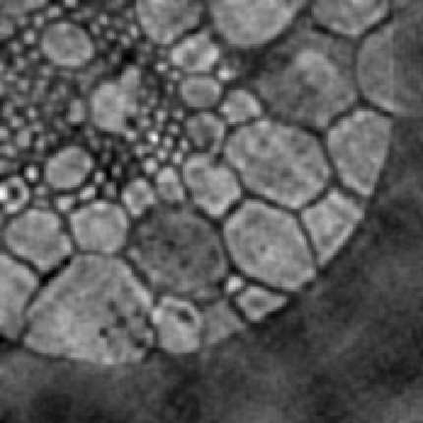
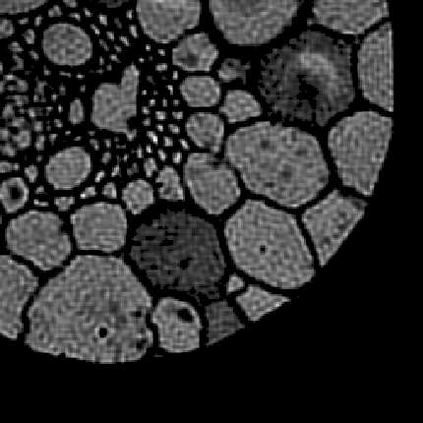
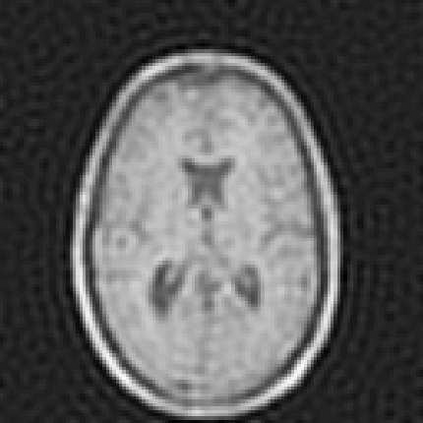
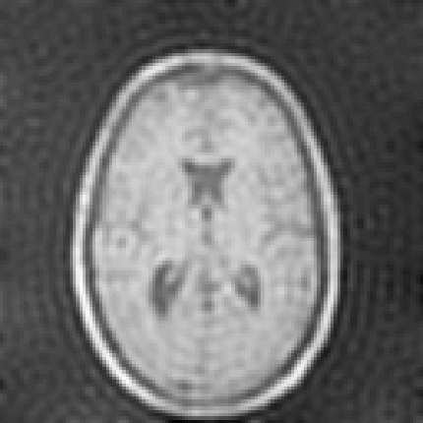
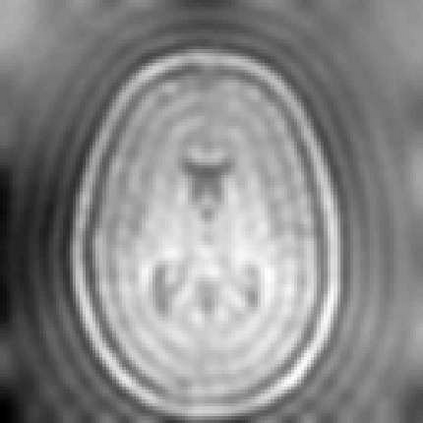
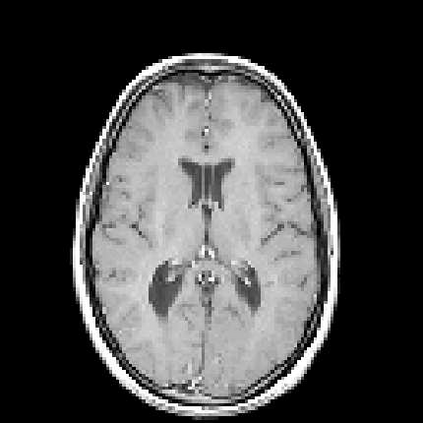
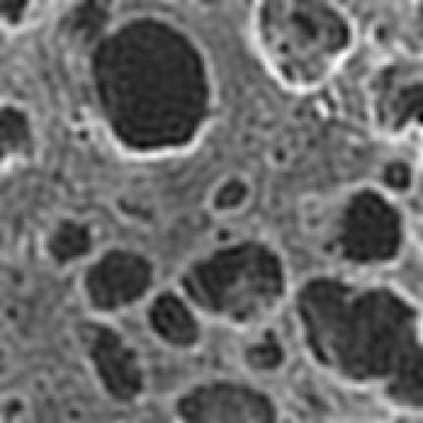
Two new hybrid algorithms are proposed for large-scale linear discrete ill-posed problems in general-form regularization. They are both based on Krylov subspace inner-outer iterative algorithms. At each iteration, they need to solve a linear least squares problem. It is proved that the inner linear least squares problems, which are solved by LSQR, become better conditioned as k increases, so LSQR converges faster. We also prove how to choose the stopping tolerance for LSQR in order to guarantee that the computed solutions have the same accuracy with the exact best regularized solutions. Numerical experiments are given to show the effectiveness and efficiency of our new hybrid algorithms, and comparisons are made with the existing algorithm.
翻译:暂无翻译